Repeated treatment failures should alert the clinician to the possibility of an otherwise inapparent immune deficiency, and a workup for this may be advised.
.... "
The goal of this publication is to support Burrascano's observations and guidelines with an analysis of a quantitative diary that carefully recorded symptom appearance over the period of more than one and a half year. The analysis includes
Applying the proposed statistical analysis to the following symptom log will reveal the presence of any of these symptom elements.
In Tab. 2 the influence of the endocrine system (menstruation cycles) and toxin levels on the activity of the immune system are summarized, as they will be interpreted later.
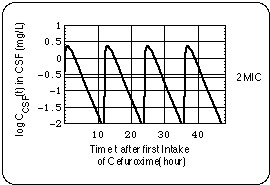
During a cefuroxime regimen i, patient experiences a net growth of the Bb population when Bb is given enough "antibiotic free time" to grow more than it was reduced under the effect of the antibiotic (antibiotic free time meaning: the time during which cefuroxime concentration in CSF is below 2 MIC). The principle of this is illustrated in a 4 day section of the cefuroxime regimen 7 displayed in Fig. 7.
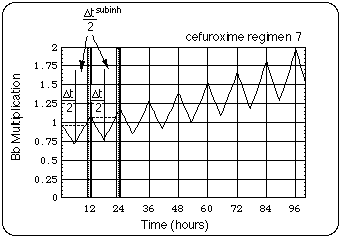
Fig. 7: Schematic of net Bb growth for cefuroxime regimen i = 7. x-axis: time after beginning of regimen 7. For illustration purposes Bb generation time was arbitrarily asumed to be equal to the in vitro generation time in the experiments of Agger et al.. Antibiotic is taken in twice daily, the time between intakes is 12 hours. Time intervals (0.5 Delta t7 = 5.5 hours per half day) with inhibitory cefuroxime concentrations in CSF (c(t) > 2 MIC) alternate with intervals (0.5 Delta t7subinh = 6.5 hours per half day) with subinhibitory concentrations (subscript 7 indicates cefuroxime regimen). Thus Bb population oscillates. Since subinhibitory levels last 1 hour per 12 hours longer than inhibitory levels (see shaded area), Bb population undergoes a net growth during 2 hours per day: t7net = Delta t7subinh - Delta t7 = 2 hours/day.
In order to plot Fig. 7 we had to assume a Bb generation time TBb. For illustration purposes, we chose the in vitro generation time TBb = TBbin vitro = 11 hours, a generation time that can be extracted from the in vitro kill kinetics experiments by Agger et al. and a similar time from Preac-Mursic et al., 1987, Preac-Mursic, et al., 1996 and Pollack RJ, Telford SR 3rd, Spielman A.. Note that this value is not applicable to an in vivo Bb population. Below we will come up with an estimate of an upper boundary for the in vivo generation time.
The daily net growth time is the sum of the contributions of the two half days, represented by the two shaded areas in Fig. 7:
t7net = 2 hours per day.
The total net growth time during regimen 7 is the sum over the n7 = 37 days of that regimen:
total net growth time = n7 t7net = 74 hours..
For an arbitrary cefuroxime regimen i the net growth time is, correspondingly,
total net growth time = ni tinet.
IV. 2 Results
The results of the corresponding calculations will be displayed in 3 ways, two of which avoid the assumption of an in vivo Bb generation time, TBb :
- a table (Table 3) giving the net Bb growth time (hours per day) during the various cefuroxime regimens,
- a diagram showing the upper envelopes of the growth curves of the type demonstrated in Fig. 7 and how they depend on the in vivo Bb generation time.
- a diagram displaying how the growth of the Bb population during the cefuroxime period depends on the in vivo Bb generation time.
The first 5 columns of the following Table 3 specify the cefuroxime regimens. The last 2 columns give the results of the calculations, i.e the number of hours per day during which cefuroxime reduced the Bb population, Delta ti, and the number of hours per day during which the Bb population was able to actually grow, tinet.
Table 3: Net Bb growth times for employed cefuroxime regimens
Cefuroxime
Regimen
i
(-)
|
Dose
D
(g/d)
|
Days
of Symptom
Log
|
Number
of Days
ni
(-)
|
Peak
Plasma
Concentration
(mg/L)
|
Delta ti for
C(t)>2 MIC in CSF
(h/d)
|
Net Growth
Time tinet
(h/d) |
| 1 |
0.5 x 1 |
168 - 182 |
15 |
2.0 |
0 |
24 |
| 2 |
2 x 1 |
183 - 192 |
10 |
8(*) |
4 |
16 |
| 3 |
2 x 2 |
193 - 202 |
10 |
8(*), 22(*) |
9 |
6 |
| 4 |
3 x 2 |
203 - 210 |
8 |
10, 28 |
10 |
4 |
| 5 |
5 x 2 |
211 - 223 |
13 |
22(*), 59 |
12 |
0 |
| 6 |
0 |
224 - 229 |
6 |
0 |
0 |
24 |
| 7 |
2 x 2 |
230 - 266 |
37 |
22(*), 22(*) |
11 |
2 |
| Average |
not appl. |
168 - 266 |
99 |
not appl. |
7.8 |
8.5 |
Comment:
ni is the number of days during which dose D was taken in,
Peak Plasma Concentrations is peak cefuroxime concentration in plasma after each intake,
Delta ti is the number of hours per day during which cefuroxime concentration was higher than 2 MIC,
Net Growth Time is the number of hours per day during which the population could undergo a net growth (a growth outweighing the loss during Delta ti).
0.5 x 1 means: 0.5 g taken in once per day.
(*) means: value determined in lab, all other peak concentrations are these values scaled according to dose and bioavailability.
The last row characterizes the entire cefuroxime period:
- the average inhibitory period Delta tav is defined as
Delta tav = n1 Delta t1 + n2 Delta t2 + .... + n7 Delta t7 / (n1 + n2 + ... + n7) = 7.8 hours per day.
- the average net growth time tavnet is defined as
tavnet = n1 t1net + n2 t2net + .... + n7 t7net / (n1 + n2 + ... + n7) = 8.5 hours per day,
so that the total number of hours during which cefuroxime was present in the CSF at subinhibitory concentrations is
ttotalnet = tavnet (n1 + n2 + ... + n7) = 812 hours = 34 days.
Fig. 8 is a more obvious way of visualizing Bb multiplication during the succession of cefuroxime regimens 1 - 7 than the Table 3, but it needs the assumption of an in vivo Bb generation time TBb. Bb population growth has been calculated for a range of these (see right margin of Fig. 8).
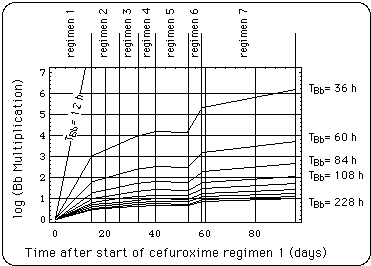
Fig. 8: Bb multiplication as a function of time, expressed as day after the start of the symptom log. In vivo Bb generation time TBb is used as curve parameter (12 h < TBb < 228 h). If net Bb growth time tinet was 24 h per day during all regimens, all growth curve segments would have a slope equal to the slope in regimen 1 or 6.
Fig. 9 is a plot of the multiplication of the Bb population over the entire cefuroxime period (days 168 - 266) versus Bb in vivo generation time. The diagram allows the reader to enter his/her guess of the multiplication necessary to bring about a (health status dependent) worsening of the infection noticeable by the patient and read the corresponding in-vivo Bb generation time off the x-axis (dashed lines demonstrate this for a Bb multiplication by a factor of 100. For a rationale of the factor 100 see e.g. Straubinger, 2000).
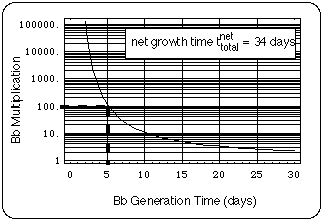
Fig. 9: Bb multiplication in cefuroxime regimens 1 - 7 equaling 34 net days of Bb growth (Bb-multiplication = exp[34 days ln2 / TBb]). Let us assume that an increase of the Bb population by at least a factor of 100 is needed for the patient to notice a worsening of her health status. Then, the upper limit of the in vivo Bb generation time would be 5 days (see dashed lines).
The next chapter will give
- a basic mechanism leading to the periodicity in the symptom occurrence, both before and during the intake of antibiotics, and
- an interpretation of the ratio of in vivo to in vitro generation time, TBb/TBbin vitro.
V. Compartment Model Displaying Symptom Cycles
We will procede here analogously to a treating physician who associates a disease with a clinical picture as it presents itself by such overall parameters as body temperature or antibody spectrum in a body compartment.
A multitude of microbiological and immunological processes (as e.g. reviewed by Rupprecht et al., 2008) work together to produce the overall, observable behavior. Similarly as the physician does not need to link the details of the individual processes to his interpretation of the dynamics of his patient's illness, we attempt to
- represent the symptom cycles by the feedback model described in this section and
- tailor the therapy correspondingly.
An immune system ("oscillatory immune system") with the following two properties develops the above analyzed symptom flare cycles, i.e. self-organized oscillations between a symptom free and an ailing stage. These oscillations are a well known property of general feedback control systems without sufficient damping (Ball P, 1999). Oscillating immune responses have been observed in non-Lyme cases and have been modeled, the models being used to optimally direct the antibiotic intervention in a similar fashion as is done in this paper (in chronologcal order:
Dibrov BF et al. 1976, 1978,
Smirnova OA 1991,
De Boer RJ et al. 1993,
Muraille E et al. 1996,
McKenzie FE, Bossert WH 1997,
see also literature surveys
1 and
2).
- a delayed immune response.
The immune system responds to what I will abbreviate as toxins such as
- Borrelia burgdorferi (Bb),
- or immune system stimulating membranous material from the outer surface of Bb, belonging to the class of thymus-independent antigens of type 1 (TI-1 antigens), like
- perhaps some outer surface proteins (lipoproteins, Osp) and
- lipopolysaccharides, LPS (a TI-1 antigen, meaning it causes T-independent antibody production. TI-1 antigens activate B-cells via Toll like receptors, which are, in human, expressed on the surface of B lymphocytes after B-cell receptor (BCR) stimulation.)
- Bb nucleic acids,
- other fragments from killed Bb or toxins released from these,
e.g. by producing cytokines (
Beck et al. 1986
Ma et al. 1993,
Tai et al. 1994,
Sellati et al. 1996,
Frieling et al. 1997,
Burns et al. 1998,
Giambartolomei et al. 1998,
Straubinger et al. 1998,
Zhang et al. 1998, see also the result of a Medline search).
It is the cytokine levels that correlate with clinical responses (
Damas et al., 1992,
Frieling et al., 1995,
van Deuren et al., 1995).
Via molecular mimicry, also autoimmune processes can be triggered by Bb proteins (Sigal 1997, Sigal and Williams 1997, Hemmer et al.1999, Klempner et al. 1999, an ongoing study headed by Adriana Marques, Laboratory of Clinical Investigation, National Institute of Allergy and Infectious Diseases, reported in NIAID's News). T-cell subpopulations (of short-lived T-cells) responsible for autoimmune processes might persist as long as sufficient levels of such proteins are present in the host (Kuby, chapter 12, S. 305). The existence of such autoimmune processes could bring about a decoupling of infection and inflammation, both in space and time. If such processes support e.g. symptom cycles, their period may differ from the periods of cycles triggered by infectious processes. The following description refers to an immune response directed against an infection.
The immune response should be visualized as being twofold:
- clinical response, predominantly inflammatory. This first reaction happens within hours of the stimulation (Kuby, Kapitel 12, p 296, und Kapitel 13, 317 - 319).
- start-up of the toxin elimination process, apparently by the humoral response (Hu and Klempner, 1997). This follows the inflammatory response.
Both reponses start some ("lag") times after the toxin levels exceeded their specific tolerance thresholds.
- too early an end of the immune response.
The immune response ends when
- the toxin concentration has fallen below a threshold and enough time has elapsed since then for the immune system to relax,
- sufficient time has elapsed for the toxin to disappear into a niche, e.g. by invading a site "invisible" to the immune system or -if the pathogen is an active Bb population- by changing its surface through antigenic variation, or
- Bb suppresses the immune response (this is believed to happen in the initial and chronic stages of the Bb infection).
These two steps are combined into a feedback control process aiming at the elimination of the toxin.
Unlike with many other infections, the incubation time of the toxins is so short (i.e. some hours, like in viral influenza) that the immune system's memory is irrelevant (pp. 202, 447 in Kuby, 1997). Thus, steps 1 and 2 will be repeated in much the same form as long as the niches release new toxins into compartments under immune system surveillance. The feedback control system is locked into undamped oscillations.
- Their amplitude (the symptom severity) decreases when the niches inject less toxin, e.g. when they run out of toxin after their Bb populations have been killed.
- Their frequency (or the time between flares) depends on many parameters of the feedback control, not just on the generation time of the spirochete. In fact, even a population of dead Bb, of TI-1 antigens like LPS or perhaps some Osp, in the niches produces proinflammatory cytokines (Straubinger et al. 1998) and is therfore able to drive such oscillations of the immune system activity.
As is illustrated in Fig. 10, the basic building blocks of the immune response model are
- the immune system switching function, f(C(t), t).
It has properties 1 and 2 of the immune system .
- the compartments.
They represent those parts of the host in which toxin levels develop. I will visualize the system of interconnected compartments as a linear system of first order differential equations.
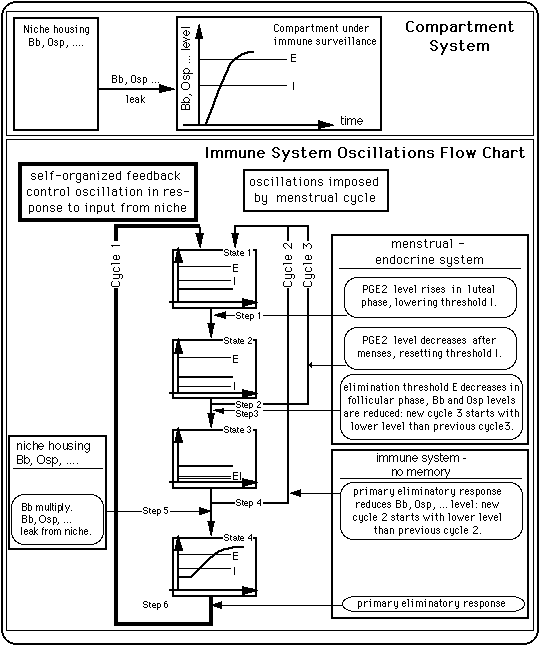
Fig. 10: A simple compartment system and an immune system control scheme that produces oscillations between an inflamed state and a symptom free state.
- Upper part: simplest possible compartment model displaying oscillations consists of a compartment under immune observation (on the right, it will alo be called "visible") and a compartment poorly visible to the immune system (the "niche" (on the left side), literature supporting the concept of a niche).
- Lower part is a flow diagram of the system behavior as a function of
- the Bb (fragment) concentration within the compartment under immune surveillance and
- the influx of Bb (fragments) from the niche (see bottom left compartment).
Like the right diagram in the upper part of the figure, the diagrams in the lower part of figure represent Bb (fragment) concentration in the compartment under immune surveillance as a function of time (heavy line and heavy curve). There is one diagram for each step of the cycles.
- Cycle 1 comprises four states,
- cycle 2 three, and
- cycle 3 consists of only the first two states.
I and E are the thresholds determining the branching of the system behavior. They are functions of the menstrual-endocrine system, e.g. the prostaglandin E2 level, and other immune system parameters, e.g. levels of modulating pleiotropic, redundant and antagonistic cytokines (Kuby, Kapitel 13, p 315). The legend in the box on the right of each transition from one state to the next specifies these influences of the endocrine and the immune system at the various steps of the symptom cycles.
-
Feedback control oscillations organized by the immune system itself (cycle 1, left part of flow chart)
- State 1: Residual level of Bb (fragments) lies below thresholds for inflammation (I) and elimination (E).
- Step 5: Due to heavy influx of Bb (fragments) from niche, Bb (fragment) level rises rapidly above thresholds I and E (state 4). The variations of I and E possibly introduced by the menstrual-endocrine system at steps 1 - 4 are negligible.
- Step 6: Immune system eliminates Bb (fragments) and returns to state 1.
-
State 1: After Bb (fragment) level has been reduced below thresholds I and E, immune system relaxes without having produced memory cells [as e.g. shown by Elsner, Hastey and Baumgarth, 2015; Hastey, Elsner, Barthold and Baumgarth, 2012]. Thus, the next time state 4 is arrived at, the immune system starts an entirely new response, never learning from the past.
- Immune response cycles imprinted by the menstrual cycle:
-
No elimination of toxins (cycle 3, right side of flow chart)
-
State 1: A residual level of Bb (fragments) ranges below thresholds I and E.
-
Step 1: In the luteal phase of the menstrual cycle the endocrine system shifts threshold I below the Bb (fragment) level (state 2), and an inflammation (with concomitant illness symptoms) develops.
- Step 2: After the endocrine system has turned off the inflammation by shifting threshold I back up, the symptom free state 1 is arrived at again.
-
Removal of toxins (cycle 2, right side of flow chart)
- State 1: Initial, symptom free state (as in cycle 3).
- Step 1: Luteal phase inflammation threshold lies below Bb (fragment) level, and illness symptoms develop (state 2, as in cycle 3).
- Step 3: With the onset of the menses threshold E is lowered and Bb (fragments) start becoming eliminated (state 3).
- Step 4: Endocrine system switches thresholds E and I back to original values, and illness symptoms disappear as state 1 is arrived at again, albeit with a lower Bb (fragment) concentration. This way, each cycle reduces the residual Bb (fragment) level. As in the self-organized mode, the immune system has no memory of the inflammation in the preceeding cycles.
Summary of immune response model:
- Cycle 1: As long as the niche heavily injects part of its content into the compartment visible to the immune system, the system is locked in self-organized feedback control cycles.
- Cycles 3 and 2: When the niche becomes isolated, i.e. ceases to inject Bb (fragments), and the "visible" Bb (fragment) level has fallen to low enough values, an inflammation surfaces only when the tendency for inflammation is elevated in the luteal phase of the menstrual cycle (Leslie et al 1994). Successive menses further reduce the Bb (fragment) level.
Thus, the compartment model
- will not give an interpretation of the microbiological and medical mechanisms behind the immune switching function,
- but will illustrate how some properties of flare cycles depend on model parameters, such as (links point to Notation section for explanation of symbols used)
- in vivo and in vitro Bb generation times (TBb and TBbin vitro, respectively),
- elimination kinetics and thresholds characterizing the immune system (TIBb, TIF, f(C, t), C1, lag time),
- threshold concentrations of Bb or fragments of (killed) Bb above which symptoms are experienced (C2),
- rate at which a Bb niche population enters the subsystem of the host responsible for the considered symptom (r(t))
Sections V. 1 and V. 2 will give simple examples of possible feedback control cycles (cycles of type 1). The mechanism driving the cycles in the absence of antibiotics are different from the one responsible for cycles under the influence of antibiotics.
V. 1 No antibiotics present
Fig. 11 shows a compartment model and the symptom cycles produced by an oscillatory immune system. The concentration C(t) of the substance invoking immune response is assumed to be proportional to the Bb concentration.
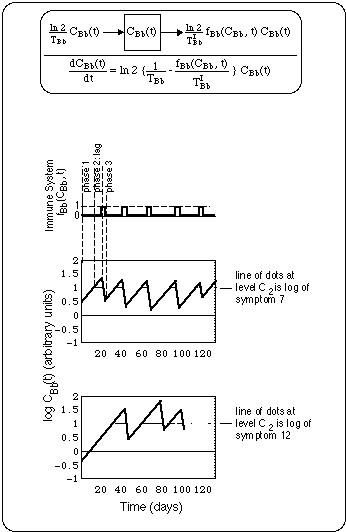
Fig. 11: Schematic of flare cycles driven by oscillatory immune response fBb(CBb(t), t), where
- CBb(t) is the time dependent concentration of Bb in the body compartment considered,
- fBb(CBb(t), t) describes the immune response as a function of the Bb concentration in the compartment. f is a function of time t itself, not only of the Bb concentration.
- fBb(CBb(t), t) = 0, when the immune system sees no Bb, i.e. as long as CBb(t) < C1 (startup threshold) and as soon as CBb(t) < C2 (shutdown threshold).
- fBb(CBb(t), t) = 1 as soon as Bb concentration exceeds the immune system startup tolerance threshold C1, i.e. when CBb(t) > C1, and as long as it stays above the shutdown tolerance threshold C2.
- t is the time variable.
The immune response is calculated with the compartment model shown in top part of figure (with a program written in Mathematica):
- The box is the body compartment under consideration.
- In this compartment the Bb concentration grows exponentially with the rate log[2]/TBb, where TBb is the in vivo Bb generation time (which is possibly compartment specific).
- The immune system reduces the Bb concentration, when Bb concentration is in excess of a threshold concentration C1 = C2. The rate of Bb elimination is assumed to be proportional to the Bb concentration the immune system sees, i.e. TIBb CBb, where the Bb elimination half life TIBb is again possibly compartment specific.
The mathematical model is displayed below the box model representation.
Note the logarithmic concentration scale in diagrams for C(t): A straight line up (down) represents exponential growth (decay).
Immune system always starts up (f = 1) when Bb concentration has reached a concentration C1. Thus, the immune system being triggered by Bb concentration, always lags behind Bb growth.
Immune system always shuts down (f = 0) at Bb concentration C2, i.e. before all Bb have been eliminated. To simplify the figure, thresholds C1 and C2 have been assumed to coincide.
f has been chosen symptom specific, assuming that immune system has localized properties. f's are chosen such that logs of symptoms 7 and 12 are reproduced (see symptom logs placed at level C2).
Data used in calculations for illustration purposes
- TBb = 7 days,
- TIBb = 0.7 days.
- C2 adjusted to fit symptom log data.
The phases of a flare cycle are:
- Bb population grows unnoticed by immune system.
- Immune system selects suitable antibodies (lag phase).
- Immune system eliminates Bb until Bb population disappears from its sight.
- The new Bb population grows unnoticed by immune system (phase 1, again).
Each zig-zag cycle represents a Bb population that "catches the immune system by surprise".
In Fig. 11 we have fitted the compartment model to the symptom cycles by allowing a variation of the location of the peaks of the immune system switching function fBb(CBb(t), t), while keeping the Bb generation time TBb and the elimination half life TIBb fixed (thus the widths of the peaks are constant). This results in shifting fixed zig-zag segments (one branch going up the other going down) around. We did not succeed fitting the data of a symptom log by doing the reverse, i.e. keeping the f-curve fixed while adjusting the slopes of the individual zig-zag branches. Thus, it seems that the times when the immune system loses track of a Bb population and starts seeing the next one are variable.
The geometry of the curves in Fig. 11 lets us see the following properties of symptom cycles before antibiotic treatment:
- When the Bb population grows (the zig-zag curve tending generally upward), flare cycles melt together with increasing time (days 60 - 100 in bottom diagram), and therefore conversely, when Bb population decreases, flare cycles "melt away" with time.
- Shifting the threshold C2 changes the fraction of the cycle during which the symptom is felt, but does not change the length of the cycle.
- As is typical for the pre-treatment time of an infection, the exponential growth of the bacteria population is so fast, leading quickly to high concentrations before it is stopped by the immune system, that there is not much doubt in the patient's subjective impression as to whether a symptom occurs or not.
During antibiotic treatment the spirochete population growth is at most proportional to time. One can see this, when looking at the symptom log, as will be demonstrated with the following model.
V. 2 Presence of antibiotics
Fig. 12 shows the properties of a compartment system applicable when a cell wall antibiotic is present. The system consists of three coupled parts:
- a source r(t) of Bb. It resides in a niche that shields it from the antibiotic. This source feeds
- the pool of spirochetes, concentration of Bb is CBb(t). The pool is exposed to the cell wall antibiotic, which creates Bb fragments whenever a spirochete enters its cell division phase. This feeds
- the pool of Bb fragments, the concentration of which is CF(t).
If the source r(t) contains only Bb fragments, it feeds the fragment compartment directly, i.e the Bb pool in Fig. 12 is missing.
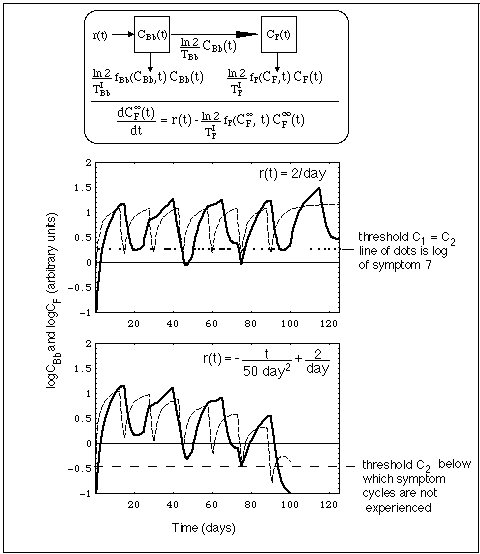
Fig. 12: Concentration CBb(t) of Bb population outside niche (dashed line) and CF(t) of Bb fragments (heavy line) resulting from a Bb source r(t). Concentrations are calculated with compartment model shown in top of figure.
- Left compartment: Bb population outside niche, concentration CBb(t),
- right compartment: Bb fragment inventory, concentration CF(t),
- differential equations equivalent with compartment system, and
- the corresponding Mathematica program.
- The equation below the compartment model (top part of figure) gives the fragment concentration when the Bb compartment has reached equilibrium for slowly varying r(t), i.e. at times when the dashed curve approaches a horizontal line.
Like in Fig. 11, f is the immune switching function, while C1 and C2 are the immune response start up and shut down thresholds, respectively.
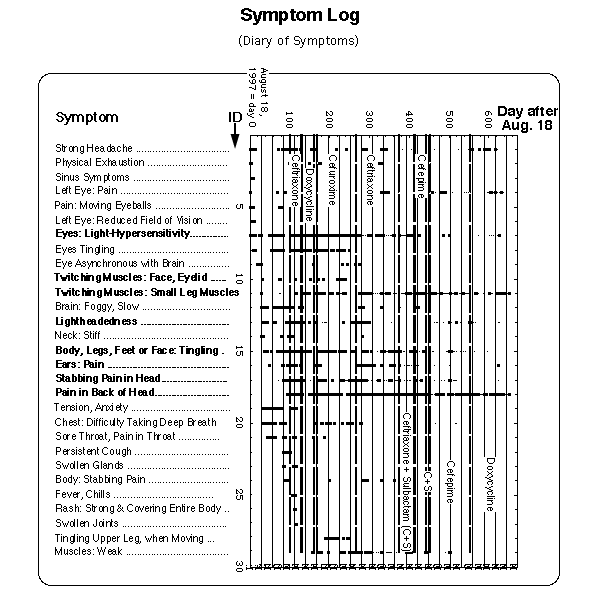
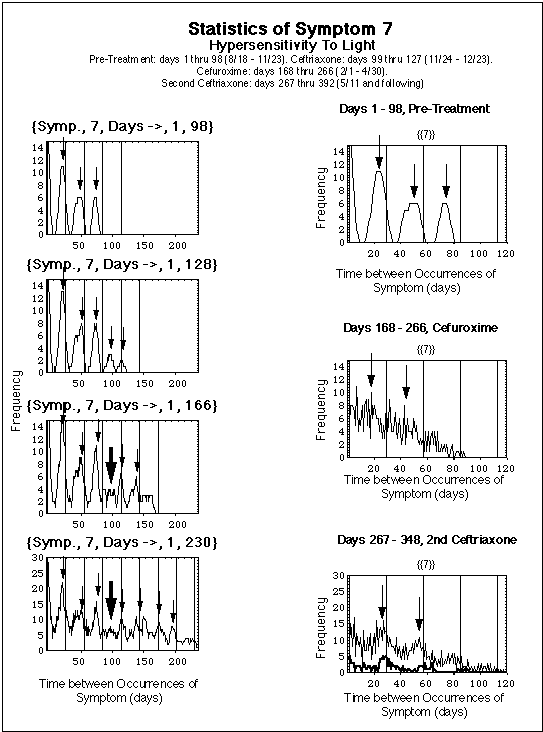
Superimposed on the concentration curves in the upper diagram at level C2 is a section of the symptom log of symptom 7, i.e. the vertical series of dots for symptom 7 (Light Hypersentisitivity) between day 272 and 292 in Fig. 1.
In the case depicted in Fig. 12,
- the Bb compartment receives continuous influx of spirochetes from niche population.
- Bb source r is constant in upper diagram and
- steadily decreasing in lower.
- Antibiotic kills fraction ln2/TBb of CBb(t) per unit time, creating Bb fragments (see arrow connecting compartments). For demonstration purposes it suffices here to oversimplify the relationship between number of killed Bb and clinical symptoms:
- each killed Bb releases one antigen molecule, e.g. LPS or Osp, (Tables 2 and 3 in Hurley 1992),
- the highly non-linear relationship between LPS or Osp concentration and clinical symptoms is replaced by a linear one.
- Both pools are subject to immune system clean-up (arrows pointing downward from compartments), and -if this is oscillatory- will go through cycles, much as the Bb pool in the system in Fig. 11 did.
- For illustration purposes, towards end of time coverd in upper diagram it is assumed that immune system loses track of Bb population (dashed curve approaches an equilibrium level). Thresholds C1 and C2 are assumed to coincide to simplify diagrams, as in Fig. 11.
Data used in computations
TBb = 5 days.
TIBb = 0.5 days.
TIF = 1 day.
r(t) as stated in upper right corner of diagrams.
Specific properties of this system are:
- No-Memory Hysteretic Immune Response
When the fragment concentration exceeds a threshold C2, this induces an (Herxheimer-like) immune reaction accompanying the fragment clean-up (Hurley 1992). The reaction subsides -as does the clean-up- once the fragment concentration has fallen below some other threshold (hysteresis). The relationship between C2 and the immune response (cytokine production) is highly non-linear, including a lag phase at the beginning (Frieling et al. 1997).
- Symptoms Development: Exponential for Active Bb
Only when the cell wall antibiotic is present at the minimum inhibitory concentration or some small integer multiple of it, the Bb pool cannot grow exponentially, not even in the absence of an immune response. When the antibiotic concentration is subinhibitory allowing the Bb population to grow exponentially, the symptoms worsen and their temporal development reflects this (see Fig. 11). Since during the time of the treatment with cefuroxime the patient experienced this worsening (see Fig. 8), we have a strong indication that active Bb have survived the 30 days of ceftriaxone and subsequent 30 days of doxycycline treatment (days 99 - 166).
- Abating Flare Cycles
The minima of the fragment compartment concentrations oscillations follow roughly an asymptotic curve, the differential equation of which is given in the box in the top of Fig. 12. The theoretical background is given in the Notation Section. Fig. 12 shows that the Bb concentration oscillates between two equilibrium levels. Only if these tend towards zero, will the infection be cured. For that the source of Bb must eventually be stopped (r(t) -> 0, see lower diagram in Fig. 12), which demands an elimination of the niche population.
- Beats
When the immune responses switching functions fBb and fF do not have the same frequency, the fragment concentration, being driven by the Bb concentration, shows a beat-like behavior in time. Correspondingly, the time during which this concentration is above a threshold level C2 shows these beats, too. This provides a simple interpretation of apparently irregular symptom logs (probably there are more involved reasons for these irregularities, including spontaneous and induced statistical fluctuations in the host's immune system). As an illustration, the log of symptom 7 is superimposed on the beats of CF(t). The log's irregularities are roughly reproduced by the modeled beats, and the fit could be improved by further shifting the periods of the two immune response functions.
Thus, a Bb populations entering the system from niches drive flare cycles, much like dust entering into a room from an outside source makes periodic room cleaning necessary. As long as there exists the dust source outside, we need to periodically clean the room. Similarly, the Bb niche population is called "active" by J.J. Burrascano as long as the Bb fragment concentration oscillates across the threshold for a Herxheimer reaction, CF(t) > C2.
The model explains an interesting feature consistent with that analogy:
- Near the end of a successful antibiosis the patient automatically lowers threshold C2 on a logarithmic scale, soon arriving at a point where this threshold dives below the minima of the oscillating fragment concentration (lower part of Fig. 12), and the symptom free days disappear.
- If the illness is improving, the fragment concentration oscillations have the general downward tendency shown in the lower diagram of Fig. 12. Then, some time after the patient has inadvertantly lowered threshold C2, the oscillations will cross the lower level C2 again, and cycles reappear. If their severity is smaller than at earlier times, this confirms the assumption of illness improvement.
- When the patient lowers C2 again, the sequence (1) - (2) is repeated. It is important that the severity of symptoms decreases during this repetitive process, otherwise the reappearance of cycles would signal a failure to eradicate the Bb source (and with it the Bb niche population), as is exemplified in the upper diagram of Fig. 12.
VI. Conclusions
The presented method of statistical evaluation enhances the visibility of flare cycles if the data basis is sufficiently large. The structure of flare cycles is analyzed on the basis of simple compartment models. The parameters of the models are related to mechanisms in the medical microbiology of an active inflammationwith Bb, based on some rough understanding of the system. Once this link to modern medical research has been strengthened, possibly improving the compartment models in unison with the medical research, this analysis will probably be a further help in making decisions concerning the necessary medication during the course of the inflammation.
The method is exemplified with the data of a female patient's symptom log. Specifics of this log are:
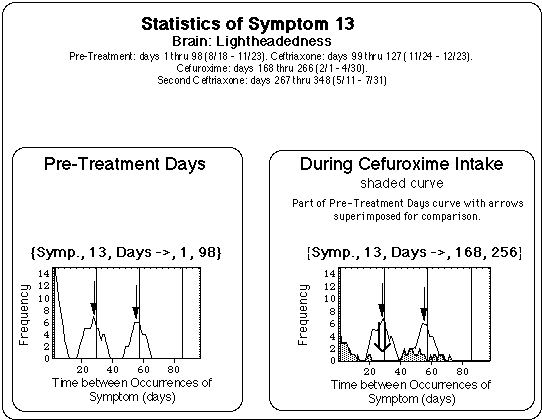
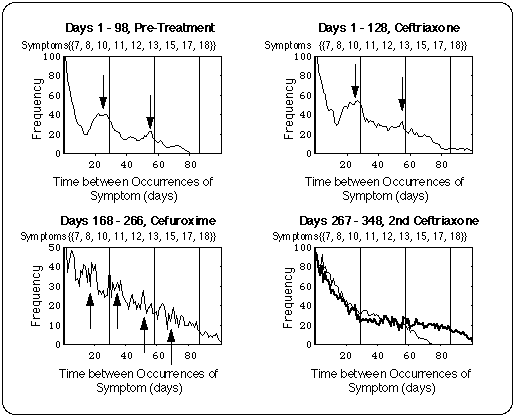
- Pre-treatment (98 days): Flare cycles between 24 and 28 days length are present prior to treatment.
- Cefuroxime (99 days):
- The length of the cycles shifted from 24 days to about one half of that (15 + or - 5 days).
- According to the symptom log, symptom severity and duration did not generally decrease.
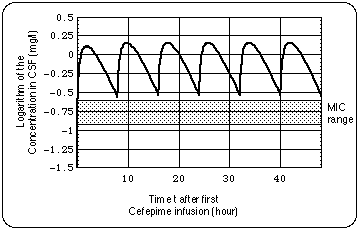
- Borrelia burgdorferi (Bb) in the CSF were exposed to twice the Minimum Inhibitory Concentration of cefuroxime (MIC = 0.13 mg/l) for less than 30 % of the day.
- If the supposed treatment failure is traced back to a growth of the Bb population in the CNS due to subMIC cefuroxime exposure, our analysis allows us to extract an upper boundary for the Bb generation time (5 days).
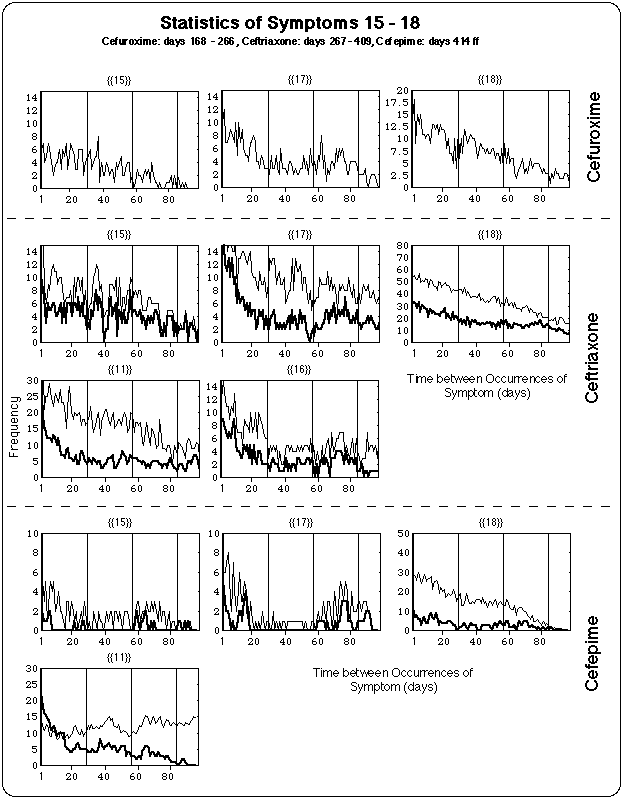
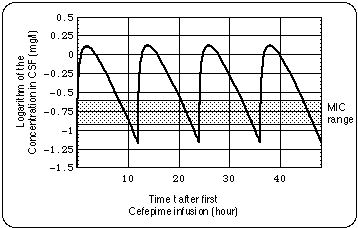
- Ceftriaxone (150 days), Cefepime (126 days) : During these infusions
- the lengths of the cycles were in the same range as during cefuroxime intake,
- the duration and severity of the symptoms decreased as compared with the cefuroxime regimen.
Some medico-microbiological interpretation of the evolution in time of the patient's flare cycle structure is given with the help of two compartment models, and needs critique and improvement from the medical research community.
The models use as input
- functions f describing the activity of the immune system (f = 1: immune response is "on", f = 0: no immune response). The immune response f switches from 0 to 1 and reverse when compartment concentrations or times cross adjustable thresholds. These would also include the typical time span Bb needs for its antigenic variation.
- guesses of the time constants describing Bb in vivo growth and decay (TBb, TIBb) and the rate of leakage of Bb or Bb fragments from the niche into compartments under immune surveillance.
As long as the niches leak, the Bb (fragments) keep contaminating
the compartments under immune surveillance and trigger a clean-up by the
immune system.
- The reason for the ongoing immune system's oscillation
between "on" and "off" is the missing memory effect, a charcteristic of
the LPS and perhaps some Osp's.
- After the long therapy with cephalosporins the flare cycles synchronize with the menstrual cycle of the patient, the symptoms occurring predominantly in the luteal phase, in which the level of the proinflammatory prostaglandin E2 is elevated (Leslie et al 1994). This is interpreted as an indication of the pathogen level being very low and possibly within the immune system's self-help range.
The results of the model seem to be stable against reasonable variations of input parameters (2), but their relative contributions, i.e. the effect of the immune system relative to the antibiotic (expressed as arrows in Fig. 12), needs to be discussed further. Once the immune system switching function f thresholds can be deduced from medico-microbiological principles, therfore not needing to be adapted to get the modeled symptom logs fit the data (as done in this analysis), the presented -rather empirical- interpretation of the infection's flare cycles would be markedly improved.
Agger WA, Callister SM, Jobe DA, In vitro susceptibilities
of Borrelia burgdorferi to five oral cephalosporins and ceftriaxone, Antimicrob
Agents Chemother 1992; Aug;36(8):1788-90.
Ball P, The self-made tapestry: pattern formation
in nature, Oxford University Press, Oxford, New York, Tokyo, 1999. (look inside book)
Barkley M, Harris N, Szantyr B, 1997. The
Lyme Urine Antigen Test (LUAT) during antibiotic therapy in women with
recurrent menstrual cycles. 10th Annual Int. Conf. on Lyme Borreliosis,
National Institute of Health, Bethesda, MD, April 28-30.
Beck G, Habicht GS, Benach JL, Coleman JL, Lysik RM, O'Brien RF,
A role for interleukin-1 in the pathogenesis of Lyme disease.
Zentralbl Bakteriol Mikrobiol Hyg [A] 263(1-2):133-6 , 1986.
Bingen E, Goury V, Bennani H, Lambert-Zechovsky
N, Aujard Y, Darbord JC, Bactericidal activity of beta-lactams and
amikacin against Haemophilus influenzae: effect on endotoxin release. J.
Antimicrob. Chemother. 30:165-172, 1992.
Bleiweiss JD, When
to Suspect Lyme Disease?
Bransfield RC, Sex
& Lyme.
Bristol-Myers Squibb, Pharmaceutical Information,
777 Scudders Mill Road Plainsboro, NJ 08536, Tel.: +1 (609) 252-4000 or
(800) 332 - 2056.
Brorson O, Brorson SH, In
vitro conversion of Borrelia burgdorferi to cystic forms in spinal fluid
and transformation to mobile spirochetes by incubation in BSK-H medium.
Infection 26:144-150, 1998.
Bericht des Landeshygiene-Instituts Mecklenburg-Vorpommern,
Schloßstraße 8, D - 17235 Neustrelitz, Tel. + 49 -3981- 272
- 100 (Dr. Kober), 1997.
Burns MJ, Furie MB, Borrelia
burgdorferi and Interleukin-1 Promote the Transendothelial Migration
of Monocytes In Vitro by Different Mechanisms, Infect Immun 66: 4875-4883,
1998.
Burrascano JJ, The
new Lyme disease: diagnostic hints and treatment guidelines for tick-borne
illnesses.
Buxton Hopkin DA., Too rapid destruction
of gram-negative organisms. Lancet i:603-604, 1977.
Chambers HF, Hadley WK, Jawetz E,
"Beta-lactam antibiotics & other inhibitors of cell wall synthesis",
pages 725-726 in: Basic & Clinical Pharmacology (Katzung BG, ed.),
Appleton & Lange, Stamford, CT, USA, 1998.
Cohen J, and McConnell JS, Antibiotic-induced
endotoxin release. Lancet i:1089-1090, 1985. (Letter).
Cohen, J, and McConnell JS, Release of endotoxin
from bacteria exposed to ciprofloxacin and its prevention with polymixin
B. Eur. J. Clin. Microbiol. 5:13-17, 1986.
Crosby HA, Bion JF, Penn CW, and Elliott TSJ,
Antibiotic-induced release of endotoxin from bacteria in vitro. J. Med.
Microbiol. 40:23-30, 1994.
Coyle, PK, Borrelia burgdorferi infection:
clinical diagnostic techniques. Immunol Invest 1997 Jan; 26(1&2):117-128
Damas P Ledoux D, Nys M , Vrindts Y, De Groote
D, Franchimont P, and Lamy M., Cytokine serum level during severe sepsis
in human IL-6 as a marker of severity. Ann. Surg. 215:356Ð362, 1992.
De Boer RJ, Perelson AS, Kevrekidis IG, Immune network behavior--I. From stationary states to limit cycle oscillations., Bull Math Biol 55(4):745-80, 1993.
Dever LL, Torigian CV, and Barbour AG,
In
Vitro activities of the everninomicin SCH 27899Êand other newer antimicrobial
agents against Borrelia burgdorferi, Antimicrob Agents Chemother. 43(7): 1773-17, 1993.
Dibrov BF, Livshits MA, Vol'kenshtein MV, Mathematical model of the immune response, Biofizika 1976 Sep-Oct;21(5):905-9, 1976.
Dibrov BF, Livshits MA, Vol'kenshtein MV, Mathematical model of the immune response. IV. Threshold character of the infectious process, Biofizika 1978 Jan-Feb;23(1):143-7, 1978.
Dotevall L, Alestig K, Hanner P, Norkrans
G, Hagberg L, The use of doxycycline in nervous system Borrelia burgdorferi infection. Scand J Infect Dis Suppl 1988;53:74-9.
Dotevall L, Hagberg L, Penetration of
doxycycline into cerebrospinal fluid in patients treated for suspected
Lyme neuroborreliosis. Antimicrob Agents Chemother 1989 Jul;33(7):1078-80.
Eng RHK, Smith SM, Fan-Havard P, and Ogbara T,
1993. Effect of antibiotics on endotoxin release from gram-negative bacteria.
Diagn. Microbiol. Infect. Dis. 16:185-189.
Evans ME, Pollack M, Effect of antibiotic
class and concentration on the release of lipopolysaccharide from Escherichia
coli. J. Infect. Dis. 167:1336-1343, 1993.
Fallon BA, Nields JA, Microbiology
of Borrelia burgdorferi, in: "Lyme Disease: A Neuropsychiatric Illness",
an overview, The American Journal of Psychiatry 1994;151,11:1571-1583.
Friedland IR, Jafari H, Ehrett S, Rinderknecht
S, Paris M, Coulthard M, Saxen H, Olsen K, and McCracken GH, Comparison
of endotoxin release by different antimicrobial agents and the effect on
inflammation in experimental Escherichia coli meningitis. J. Infect. Dis.
168:657-662, 1993.
Frieling JTM, Mulder JA, Hendrics T , Curfs
JHAJ, van der Linden CJ, Sauerwein RW, Differential Induction of Pro-
and Anti-Inflammatory Cytokines in Whole Blood by Bacteria: Effects of
Antibiotic Treatment, Antimicrobial Agents and Chemotherapy 35:1439Ð1443,
1997.
Frieling JTM, Van Deuren M, Wijdenes J, Van
der Meer JWM, Clement C, Van der Linden C, and Sauerwein RW, Circulating
interleukin-6 receptor in patients with sepsis syndrome. J. Infect. Dis.
171:469Ð472, 1995. (see also Frieling et al 1997)
Giambartolomei GH, Dennis VA, Philipp
MT, Borrelia
burgdorferi stimulates the production of interleukin-10 in peripheral blood
mononuclear cells from uninfected humans and rhesus monkeys, Infect
Immun Jun;66(6):2691-7, 1998.
Goodman and Gilman's "The Pharmacological
Basis of Therapeutics, 9th ed., McGraw Hill, 1995, abstracting this value
from Schaad et al., 1990.
Groer M, Carr J, Younger MS, Relationships
between self-reported symptoms of infection, menstrual-cycle-related distress,
and cycle phase. Behav Med 1993 Spring;19(1):13-9, 1993.
Hemmer B, et al. Identification of candidate
T-cell epitopes and molecular mimics in chronic Lyme disease. Nature Medicine
5(12):1375-82, 1999.
Hu LT, Klempner MS, Host-pathogen interactions
in the immunopathogenesis of Lyme disease. J Clin Immunol 17(5):354-65,
1997.
Hurley JC, Antibiotic-induced release of
endotoxin: a reappraisal. Clinical Infectious Diseases 1992;15:840-854.
Karlsson M, Hammers S, Nilsson-Ehle I, Malmborg
AS, Wretlind B, Concentrations of doxycycline and penicillin G in sera and cerebrospinal fluid of patients treated for neuroborreliosis. Antimicrob
Agents Chemother 1996 May;40(5):1104-7.
Kessler RE, Fung-Tomc J, Susceptibility
of bacterial isolates to beta-lactam antibiotics from U.S. clinical trials
over a 5-year period, Am J Med 1996;100(suppl 6A):13S-19S.
Klempner MS and Huber BT, Is it thee
or me?-autoimmunity in Lyme disease. Nature Medicine 5(12):1346-7, 1999.
Kossmann T, Hans V, Stocker R, Imhof HG,
Joos B, Trentz O, Morganti-Kossmann MC, Penetration of cefuroxime into
the cerebrospinal fluid of patients with traumatic brain injury. J Antimicrob
Chemother 37:161-7, 1996.
Kuby J, Immunology,
3rd Ed., WH Freeman and Co, New York, 1997.
Lawrence C, Lipton RB, Lowy FD, Coyle
PK, Seronegative chronic relapsing neuroborreliosis. Eur Neurol 1995;35(2):113-117.
Leslie
CA, Dubey DP, Increased PGE2 from human monocytes isolated in the
luteal phase of the menstrual cycle. Implications for immunity?, Prostaglandins
1994 Jan;47(1):41-54.
Ma Y, Weis JJ, Borrelia
burgdorferi outer surface lipoproteins OspA and OspB possess B-cell mitogenic
and cytokine-stimulatory properties. Infect Immun 1993 Sep;61(9):3843-53.
Mattie H, Antibiotic efficacy in vivo predicted by in vitro activity, Internat J Antimicrob Agents 14:91-98, 2000.
Mattman, LH, Cell
Wall Deficient Forms - Stealth Pathogens, 2nd. ed., CRC Press, 1993.
McConnell, J. S., and J. Cohen, Release
of endotoxin from Escherichia coli by quinolones. J. Antimicrob. Chemother
18:765-766, 1986. (Letter).
McKenzie FE, Bossert WH, The dynamics of Plasmodium falciparum blood-stage infection, J Theor Biol. 188(1):127-40, 1997.
Mertsola, J., O. Ramilo, M. M. Mustafa, X.
Saez-LLorens, E. J. Hansen, and G. H. McCracken, Release of endotoxin
after antibiotic treatment of gram-negative bacterial meningitis. Pediatr.
Infect. Dis. J. 8:904-906, 1989.
Mohler, J. B. Fantin, J. L. Mainardi, and C.
Carbon, Influence of antimicrobial therapy on kinetics of tumor necrosis
factor levels in experimental endocarditis caused by Klebsiella pneumoniae.
Antimicrob. Agents Chemother. 38:1017-1022, 1994.
Muraille E, Thieffry D, Leo O, Kaufman M, Toxicity and neuroendocrine regulation of the immune response: a model analysis, J Theor Biol. 183(3):285-305, 1996.
Nau R et al., Passage of cefotaxime and ceftriaxone
into cerebrospinal fluid of patients with uninflamed meninges. Antimicrob
Agents Chemother 37:1518-1524, 1993.
Northern AL, Rutter SM, Peterson CM, Cyclic
changes in the concentrations of peripheral blood immune cells during the
normal menstrual cycle. Proc Soc Exp Biol Med Oct;207(1):81-8, 1994.
Phillips SE, Mattman LH, Hulinska D, Moayad
H, A
Proposal for the reliable culture of Borrelia burgdorferi from patients
with chronic Lyme disease, even from those previously aggressively treated,
Infection 26 (1998) 364-367.
Preac-Mursic V, Wilske B, Schierz G, Holmburger
M, Süß E, In vitro and in vivo susceptibility of Borrelia
burgdorferi, Europ J Clin Microbiol 6:424-426, 1987.
Preac-Mursic V, Weber K, Pfister HW, Wilske
B, Gross B, Baumann A, Prokop J, Survival
of Borrelia burgdorferi in antibiotically treated patients with Lyme borreliosis.
Infection Nov-Dec;17(6):355-9, 1989.
Preac-Mursic V, Wilske B, Schierz G, Süß
E, Comparative antimicrobial activity of new macrolides against Borrelia
burgdorferi. Europ J clin Microbiol Infect Dis 8:651-653, 1989.
Preac-Mursic V, Marget W, Busch U, Pleterski
D, Rigler S, Hagl S , Kill
Kinetics of Borrelia burgdorferi, Infection, 24: 9 - 16, 1996.
Preac Mursic V, Wanner G, Reinhardt S, Busch
U, Marget W, Formation
and cultivation of Borrelia burgdorferi spheroplast-L-form variants.
Infection 24 (1996): 218-226.
Roumen RMH., Frieling JT M , van Tits HWHJ ,
van der Vliet JA, and Goris RJA, Endotoxemia following major vascular
operations. J. Vasc. Surg. 18:853-857, 1993.
Samples taken from 43 year old female
whose data were analyzed in this report.
Schaad UB, Suter S, Gianella-Borradori A,
Pfenninger J, Auckenthaler R, Bernath O, Chesaux JJ, and Wedgwood J,
A comparison of ceftriaxone and cefuroxime for the treatment of bacterial
meningitis in children. N. Engl. J. Med. 322:141-147, 1990.
Sellati TJ, Abrescia LD, Radolf JD, Furie MB.
Outer
surface lipoproteins of Borrelia burgdorferi activate vascular endothelium
in vitro. Infect Immun Aug;64(8):3180-7, 1996.
Schutzer SE, Coyle PK, Belman AL, Golightly
MG, Drulle J, Sequestration
of antibody to Borrelia burgdorferi in immune complexes in seronegative
Lyme disease. Lancet 1990 Feb 10;335(8685):312-315.
Schutzer SE, Coyle PK, Dunn JJ, Luft BJ,
Brunner M, Early
and specific antibody response to OspA in Lyme Disease. J Clin Invest
Jul;1994(1):454-457, 1994.
Shenep, JL, Flynn PM , Barrett FF, Stidham GL,
and Westenkirchner DF, Serial quantitation of endotoxemia and bacteremia
during therapy for gram-negative bacterial sepsis. J. Infect. Dis. 157:565-568,
1988.
Shenep, JL, Barton RP, and Mogan KA, Role
of antibiotic class in the rate of liberation of endotoxin during therapy
for experimental gram-negative bacterial sepsis. J. Infect. Dis. 151:1012-1018,
1985.
Shmuklarsky MJ, Boudreau EF, Pang LW,
Smith JI, Schneider I, Fleckenstein L, Abdelrahim MM, Canfield CJ, Schuster
B, Failure of doxycycline as a causal prophylactic agent against Plasmodium falciparum malaria in healthy nonimmune volunteers. Ann Intern Med 1994
Feb 15;120(4):294-9.
Sigal LH, Immunologic mechanisms in
Lyme neuroborreliosis: the potential role of autoimmunity and molecular
mimicry, Semin Neurol 1997 Mar;17(1):63-8
Sigal LH, Williams S, A monoclonal antibody
to Borrelia burgdorferi flagellin modifies neuroblastoma cell neuritogenesis
in vitro: a possible role for autoimmunity in the neuropathy of Lyme disease,
Infect Immun 1997 May;65(5):1722-8.
Smirnova OA, Study of cyclic kinetics of immunity by mathematical modeling methods, Kosm Biol Aviakosm Med. 25(5):53-6, 1991.
Spangler SK, Jacobs MR, Apfelbaum PC,
MIC and Time-Kill Studies of Antipneumococcal Activity of 118819X (Sanfetrinem)
Compared with Those of Other Agents, Antimicrob Agents Chemother 41:141-155,
1997.
Straubinger RK, Straubinger
AF, Summers BA, Erb HN, Härter L, Appel MJG, Borrelia
burgdorferi induces the production and release of proinflammatory cytokines
in canine synovial explant cultures. Infect Immun 66(1):246-258, 1998.
Straubinger RK, PCR-Based Quantification of Borrelia burgdorferi Organisms in Canine Tissues over a 500-Day Postinfection Period. J Clin Microbiol 2000;38:2191.
Tai KF, Ma Y, Weis JJ, 1994. Normal human B
lymphocytes and mononuclear cells respond to the mitogenic and cytokine-stimulatory
activities of Borrelia burgdorferi and its lipoprotein OspA. Infect Immun
Feb;62(2):520-8, 1994.
Thornsberry et al., In vitro activity
of cefepime and other antimicrobials: survey of European isolates, J. Antimicrobial
Chemother 32, Suppl. B, 55-62, 1993.
van den Berg C, De Neeling AJ, Schot CS,
Hustinx WMN, Wemer J, and de Wildt DJ, Delayed antibiotic-induced lysis
of Escherichia coli in vitro is correlated with enhancement of LPS release.
Scand. J. Infect. Dis. 24:619-627, 1992.
van Deuren, M, van der Ven-Jongekrijg J,
Bartelink AK, van Dalen R, Sauerwein RW, and van der Meer JW, Correlation
between proin-flammatory cytokines and antiinflammatory mediators and the
severity of disease in meningococcal infections. J. Infect. Dis. 172:433Ð439,
1995.
Wagner D private communication, Pharmaceutical
Info Div., 777 Scudders Mill Road, Plainsboro, NJ 08536, Tel.: +1 (609)
897 - 2776, Fax: +1 (609) 897 - 6042.
Yim CW, Flynn NM, Fitzgerald FT, Penetration
of oral doxycycline into the cerebrospinal fluid of patients with latent
or neurosyphilis.Antimicrob Agents Chemother 1985 Aug;28(2):347-8.
Zhang JR, Hardham JM, Barbour
AG, Norris SJ, Antigenic
variation in Lyme disease borreliae by promiscuous recombination of VMP-like
sequence cassettes, Cell Apr 18;89(2):275-285, 1997.
Zhang H, Niesel DW, Peterson JW, Gary
R, Lipoprotein release by bacteria: potential factor in bacterial pathogenesis,
Infect Immun 66(11):5196-5201, 1998.
VIII. Appendix
VIII. 1. Notation
b = bioavailability of cefuroxime relative to its biolavailability with prior food intake (b =: 1 with prior food intake). b = 1/2.7 without prior food intake, which value was the ratio of the measured peak plasma concentrations in patient's blood after cefuroxime intake without and with a prior meal (dimensionless).
Bb = Borrelia burgdorferi.
C(t) = concentration of substance provoking immune response, i.e. of Bb (CBb(t)) and of Bb fragments (CF(t)) (units: number of spirochetes per system volume).
cCSF(t) = concentration of antibiotic in CSF (units: mg/L).
cGI(t) = concentration of antibiotic in gastro-intestinal tract at time t after drug intake (units: mg/L).
CHx = threshold concentration of Bb fragments starting Herxheimer like reaction (units: number of fragments per system volume).
cP(t) = concentration of antibiotic in blood plasma at time t after drug intake/infusion (units: mg/L).
CooBb = stationary concentration of Bb population outside the niche = r(t)/(ln2 (1/TBb + 1/TIBb)) or r(t) TBb/ln2, depending on whether immune system is assumed to be eliminting Bb or not (units: number of fragments per system volume).
CooF(t) = concentration of Bb fragments after concentration CBb(t) of Bb population outside the niche has reached its stationary value CooBb (see Fig. 12) (units: number of fragments per system volume).
CSF = cerebrospinal fluid.
compartment model = a visualization of a linear system of first order differential equations describing the growth of the number of cells in a system. A system may consist of several subsystems, each of which will be represented by a compartment. Compartments have in- ond outfluxes having the dimension cells per time (when the entities within a compartment are cells). What comes out of one compartment may go into some other compatrment, the two compartments being "coupled". Each compartment is represented by a differential equation which states how much goes in and out per unit time. The Mathematica code representing the compartment models used here is given in http://www.lymenet.de/symptoms/cycles/mathcode.htm.
cytokines: Plasma LPS concentrations usually do not correlate with clinical symptoms (Roumen et al. 1993). It is the induction of cytokines through cell wall components like LPS which mediates the biological responses during bacterial infections. Cytokine levels and types of cytokines have repeatedly been shown to correlate with clinical outcome (Damas et al., 1992, Frieling et al., 1995, van Deuren et al., 1995).
C1 = threshold concentration triggering the immune system to start toxin elimination (apparently by its humoral branch). The immune response starts with a lag phase. Immune response subsides when toxin concentrations "visible" to the immune system have fallen below another threshold concentration. (units: number of spirochetes or fragments per system volume).
C2 = concentration threshold for inflammation, i.e. above which illness symptoms are perceived (units: number of spirochetes or fragments per system volume).
D = dosage of cefuroxime (gram per intake).
deltai = length of the ith menstrual cycle.
Delta t = time during which cefuroxime concentration in CSF is larger or equal a given inhibitory concentration (units: hours/day).
Delta tsubinh = time during which cefuroxime concentration in CSF is smaller than a given inhibitory concentration (units: hours/day).
equilibrium of a compartment = state in which influx to the compartment equals outflux out of it. At equilibrium the compartment is full, meaning that its concentration will no longer rise.
In particular, here are some properties of the 2-compartment system in Fig. 12:
F = subscript meaning Bb fragments.
f = free (i.e. Bb affecting) fraction of cefuroxime concentration in considered subsystem (here CSF) relative to its plasma concentration (f = : 1 for plasma), f = cCSF/cplasma = 0.1 for CSF (dimensionless). Data from
f(C, t) = dimensionless function describing the activity of the immune response ("immune switching function"). f ia either 0 ("no immune response") or 1 ("immune response").
Here, the immune response is assumed to be directed
- either against Bb, then the immune switching function will be called fBb, or
- against Bb fragments, the immune switching function then being called fF.
Depending on the system, f may depend on both C and t or on only one of these arguments, the corresponding concentration and time thresholds being C1 and lag phase tau, respectively.
flare = cluster of days with symptom occurrence.
follicular phase (here used sensu lato) = the first phase of the menstrual cycle, starting with the menstruation (menstrual bleeding) and ending with the ovulation, i.e. days 1 through 12 ... 14.
I = superscript meaning immune system.
incubation time = time between infection (entrance of the pathogen into host) and development of clinical symptoms.
Immune Response Interval = time interval of approximately 6 days duration, centered around the day of menses (beginning of menstrual bleeding), during which Barkley, Harris and Szantyr observed systematically high antigen concentrations in the urine of a Lyme patient (Barkley et al., 1997). The authors suggest that the immune system has a higher level of activity during this phase (see also testimony of M.S. Barkley before the New York State Assembly Standing Committee on Health, Public Hearing "Chronic Lyme Disease and Long-Term Antibiotic Treatment", Albany, NY, USA, 27.11.2001, pp. 199 - 227).
invisible = located in a compartment into which the immune system or the antibiotic penetrates only poorly. The table gives examples of such locations in which Bb were found.
ki = ln 2/Ti (units: 1/hour).
i =
- CSF,
- GI (gastro-intestinal tract),
- P (blood plasma).
kPCSF = transition rate for drug from plasma to CSF compartment.
lag time = lag phase (symbol: tau)
ln 2 = (natural logarithm of 2 =) 0.69.
LPS = lipopolysaccharide.
luteal phase = phase of the menstrual cycle after the ovulation.
memory = the attribute of the immune system mediated by memory cells whereby a second encounter with an antigen induces a faster start and a heightened state of immune reactivity (Kuby pp 397 - 399)
menses = day of onset of menstrual bleeding.
MIC = Minimum Inhibitory Concentration. Definition: MIC is the minimum level necessary to inhibit bacterial growth. It depends on the bacterial isolate. MIC50 and MIC90 are the levels at which 50 % and 90 % of the tested isolates are inhibited, respectively. (Critique of the "Minimum Inhibitory Concentration" concept).
MIC for cefuroxime = 0.13 mg/L, as determined by Agger et al. 2 MIC = 0.26 mg/L is used in the computations, which corresponds to MIC90 = 0.25 mg/L as determined by Preac-Mursic (1987). A critical discussion of the concept behind the MIC can be found in Mattie H 2000) See also Preac-Mursic et al 1996.
ni = number of days of a constant cefuroxime regimen (units: day).
net growth of Bb population = growth of population remaining when decay of population has been subtracted.
niches protect Bb from the immune system or the antibiotic (Preac-Mursic et al., 1989) or render toxin released by Bb "invisible" to the immune system. The protection may wane with time and so will the size of the spirochete or toxin population in the niche.
Niches are provided by the host in the form of physical compartments, but they can also be produced by Bb itself in the form of chemical or microbiological defense mechanisms (see also overview in Chapter Background Information of J.J. Burrascano's essay "Managing Lyme Disease".
- Host provided niches are sites poorly accessible to antibiotics and normal immune surveillance
Examples
- Bb might provide its own chemical and microbiological niches
- by shedding glycoprotein that forms strong complexes with antibodies (Schutzer et al., 1994), thereby enabling the organism itself to escape immune surveillance (Lawrence et al., 1995),
- by producing beta-lactamases, reducing the permeablity of the outer cell membrane or modifying the target of the antibiotic, the "penicillin binding proteins", so that the attachment of the antibiotic is reduced (Chambers et al., 1998),
- by changing its outer surface (Zhang et al., 1997), e.g. developing cell wall deficient (CWD) forms (Preac-Mursic et al. 1996). Mattman 1993 interprets the ubiquitous CWD forms of bacteria and fungi as states of a variable equilibrium between cell wall (ZW) and outer membrane (AM) dissolving and rebuilding processes, the former being driven by lysozymes of the organism itself and external stressors, e.g. antibiotics. According to Phillips et al. 1998 immune system and antibiotics shift this equilibrium in blood of Lyme patients to CWD forms. Together with the blood the CWD forms of Bb may spread throughout the host. Because the penetration of both the immune system and antibiotic into an organ (or compartment) varies from organ to organ, so will the equilibrium form of Bb. In some locations even the parent (spirochetal) form may be able to exist. Thus, the blood compartment may be thought of as a niche releasing Bb into other host compartments,
- by producing biofilms or settling in biofilms already present.
In the model simulating the flare cycles in the presence of antibiotics, the term "niche" is used in this generalized sense.
The basic concept underlying the model is that the niche has the following properties:
- The immune system or antibiotic needs long periods, possibly several months, to empty a niche.
- Since the toxins (antigen, pathogen) within a niche are only "poorly visible" to the immune system, they do not stimulate an inflammatory immune response while in the niche.
- Depending on the concentration in the niche (and other parameters), a niche releases its content into the compartments under immune system or antibiotic surveillance, the "visible" compartments responsible for the symptoms.
Osp = variable, plasmid encoded Outer sphere protein of Bb. The Osp's labeled OspA (30 ... 32 kD), OspB (34 ... 36 kD), OspC (21 ... 24 kD) are unique for Bb, as are the proteins p39 (39 kD) and p93 (93 kD).
ovulation = day on which the ripe ovum (egg cell) leaves the ovarian follicle.
prostaglandin E2 = a lipid inflammatory mediator with diverse biological activities, including increased vascular permeability and dilation, and induction of neutrophil chemotaxis (Kuby, p. 368-371).
r(t) = time variable Bb source term in compartment model (units: spirochetes per day entering unit system volume). It is assumed that r(t) varies much more slowly than concentrations C(t).
symptom = consequence of an inflammation of glial or neural tissue.
system = infected organ or tissue responsible for symptom. Basic systems are defined after Bleiweiss and have been further expanded here into subsystems characterized by the symptoms in Fig. 1 (for symptoms characteristic for borreliosis see also Cairns V, and Godwin J, Post-Lyme borreliosis syndrome: a meta-analysis of reported symptoms, International Journal of Epidemiology 2005 34(6):1340-1345).
ta = part of flare cycle during which immune system is active (units: day).
tb = part of flare cycle during which immune system is not yet active (flare cycle duration is tb + ta) (units: day).
TBb = in vivo Bb generation time (units: day).
TBbinvitro = in vitro Bb generation time. Values extracted tentatively from kill kinetics published by Agger et al. and Preac-Mursic et al. are 11 hours and 10 hours, respectively.
TBbI = Bb elimination half life characterizing immune system (units: day).
TCSF = elimination half life of antibiotic from CSF compartment (units: hour).
TFI = Bb fragment elimination half life characterizing immune system (units: day).
TGI = elimination half life for GI-tract resorption.
total concentration of drug = concentration of all chemical species of drug. Chemical species are the free drug and chemical complexes containing drug. Total concentrations are determined by breaking up all chemical complexes. (units: mg/l).
toxins are
- Borrelia burgdorferi (Bb),
- or immune system stimulating membranous material from the outer surface of Bb, belonging to the class of thymus-independent antigens of type 1 (TI-1 antigens), like
- perhapss some outer surface proteins (lipoproteins, Osp) and
- lipopolysaccharide, LPS (Coyle 1997),
- Bb nucleic acids,
- other fragments from killed Bb or toxins released from these,
These toxins produce cytokines (Ma et al. 1993, Tai et al. 1994, Sellati et al. 1996, Frieling et al. 1997, Burns et al. 1998, Giambartolomei et al. 1998, Straubinger et al. 1998, Zhang et al. 1998, see also the result of a Medline search). It is the cytokine levels that correlate with clinical responses (Damas et al., 1992, Frieling et al., 1995, van Deuren et al., 1995).
Via molecular mimicry (Kuby, Ch. 20, S. 497), also autoimmune processes can be triggered by Bb proteins (Sigal 1997, Sigal and Williams 1997). T-cell subpopulations (of short-lived T-cells) responsible for autoimmune processes might persist as long as a sufficient level of such proteins exists.
TP = renal elimination half life from plasma compartment.
t = time variable (units: hour in pharmacokinetic model, units: day in models for flare cycles, Figs. 11 and 12).
tinet = time for net growth of Bb population.
t0 = time of bolus infusion of cephalosporin (units: hour).
tau = lag time for resorption from GI tract. tau = 1.4 h, fitted from experimentally determined plasma concentrations (units: hour).
(see also lag phase in immune response.)
22.1 mg/l = peak plasma concentration measured in patient's plasma after intake of 2 gram of cefuroxime with prior meal.
xyz =: n this equation means xyz is by definition equal to n.
VIII. 2. Medication
The following table specifies the antibiotics and the periods during which they were taken. The table to the right translates "Day after August 18, 1997" into customary dates. August 18, 1997 is the day when the opticus neuritis appeared (list of symptoms).
TABLE : Antibiotic Regimes
|
DAYS
after August 18, 1997 |
ANTIBIOTIC |
DOSE PER DAY |
| 99 ... 128 |
ceftriaxone |
2 g |
129 ... 135
136 ... 159
|
doxycycline |
2 x 0.2 g
3 x 0.1 g |
168 ...182
183 ... 192
193 ... 202
203 ... 204
|
cefuroxime
|
0.5 g
2 g
2 x 2 g
2 x 3 g
|
205 ... 210
211 ... 223
|
cefuroxime
azithromycin
|
2 x 3 g
0.25 g
2 x 5 g
0.25 g
|
| 224 ... 229 |
azithromycin |
0.25 g |
230 ... 234
|
cefuroxime
azithromycin |
2 x 2 g
0.25 g |
| 235 ... 247 |
cefuroxime |
2 x 2 g
|
248 ... 266
267 ... 271
|
cefuroxime
azithromycin
|
2 x 2 g
0.25 g
2 g
0.25 g
|
| 272 ... 273 |
azithromycin |
0.25 g |
274 ... 357
|
ceftriaxone (*)
azithromycin |
2 g
0.25 g |
| 358 |
azithromycin |
0.25 g |
359
|
ceftriaxone
azithromycin |
2 g
0.25 g |
| 360 |
ceftriaxone |
2 g |
361 ... 372
|
ceftriaxone
azithromycin |
2 g
0.25 g |
373 ...396
397 ... 405
|
ceftriaxone
sulbactam
azithromycin |
2 g
2 x 1 g
0.25 g
2 x 1 g
2 x 1 g
0.25 g |
406 ... 409
|
ceftriaxone
sulbactam |
2 x 1 g
2 x 1 g |
414 ... 415
416 ... 418
420
421
|
cefepime |
3 x 2 g
2 x 2 g
2 g
2 x 2 g |
422 ... 423
424 ... 432
433 ... 439
440
|
cefepime
azithromycin
amantadine(a) |
2 x 2 g
0.25 g
0.2 g
3 x 2 g
0.25 g
0.2 g
(2 , 2, 1) g
0.25 g
0.2 g
(2, 2, 0) g
0.25 g
0.2 g
|
441 ... 451
|
ceftriaxone
sulbactam
azithromycin
amantadine(a) |
2 x 1 g
2 x 1 g
0.25 g
0.2 g |
452 ... 547
|
cefepime
azithromycin
amantadine(a) |
3 x 2 g
0.25 g
0.2 g |
| 548 ... 550 |
cefepime |
3 x 2 g |
551 ... 553
554 ... 558
559
561
562 ... 653 (**)
|
doxycycline |
2 x 0.2 g
3 x 0.2 g
0.2 g
2 x 0.2 g
3 x 0.2 g
3 x 0.2 g
|
|
855 ... 859(+)
|
ceftriaxone
|
2 g
|
|
859 ... 889 (**)
|
doxycycline
|
3 x 0.2 g
|
|
Day
after August 18,
1997
|
day. month. year
|
0
14
44
75
105
136
167
195
226
256
287
317
348
379
409
440
470
501
532
560
591
621
652
682
713
744
774
805
835
866
897
926
957
987
1018
|
18.8.1997
1.9.1997
1.10.1997
1.11.1997
1.12.1997
1.1.1998
1.2.1998
1.3.1998
1.4.1998
1.5.1998
1.6.1998
1.7.1998
1.8.1998
1.9.1998
1.10.1998
1.11.1998
1.12.1998
1.1.1999
1.2.1999
1.3.1999
1.4.1999
1.5.1999
1.6.1999
1.7.1999
1.8.1999
1.9.1999
1.10.1999
1.11.1999
1.12.1999
1.1.2000
1.2.2000
1.3.2000
1.4.2000
1.5.2000
1.6.2000
|
|
Comment
(a) Amantadin Stada 100 mg (Amantadinhydrochlorid) (in cache)
(*): every two weeks ultrasound checkups for biliary sludging (see also corresponding caveat by J.J. Burrascano).
(**): day 652 = 1. June 1999, day 894 = 29. January 2000.
(+): suspected relapse, probably induced by extreme work load (see below)
The person worked normal hours in her profession during the entire period, except for one sick leave during days 23 - 29, when a series of diagnostic tests were done in a hospital.
Relapses
- After the last but one doxycycline regime (i.e. after day 653) there were only minor symptoms left clustering mostly in the luteal phase, similar to -but less frequent and severe than- prior to day 500 (Fig. VIII.3.2).
- Period between day 855 and day 889 (21. December 1999 and 24. January 2000) was initiated by unusually heavy work load in patient's professional life. The following intense symptoms reappeared abruptly, i.e. did not develop over a period of e.g. a week (id, description of symptom). They did not increase in intensity:
- id 11: muscles in legs twitch while legs remain at rest
- id 17: stabbing pain in back of head
- id 18: pain (not stabbing) in back of head
Medication was taken prophylactically to stabilize health status. At the same time, Qi Gong was practiced diligently. When 5 days after the onset of intense symptoms it turned out that symptoms did not increase in number or intensity, ceftriaxone was replaced by doxycycline. Practice (frequency and duration) of Qi Gong was intensified when it became apparent that symptom intensity could be lowered with the help of Qi Gong. From that it was concluded that
- either there was no bacteriological basis to the relapse
- or borrelia multiplication was stemmed immediately by medication.
- As of today the person has
- had no further relapses, i.e. was -apart from mild occurrences of symptom 18 ("pain in back of head")- practically symptom free after day 660 = 9. June 1999.
- been totally without symptoms since 30. Jan. 2000, i.e. 2.5 years after the beginning of the infection.
VIII. 3. Statistical Methods
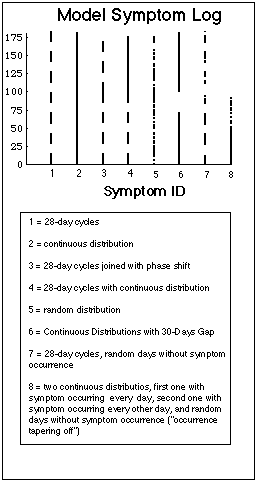
To visualize our method of statistical analysis, we have applied it to an artificial symptom log containing basic symptoms (see upper part of Fig. VIII. 3).
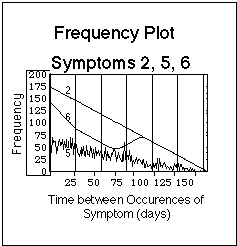
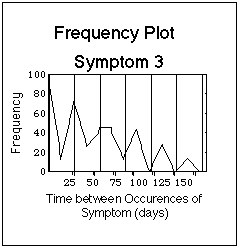
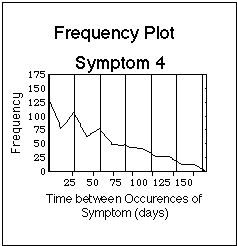
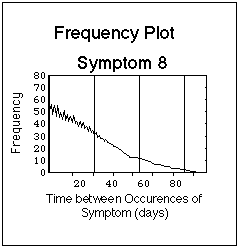
Fig. VIII.3: Artificial symptom log (upper part of Figure) containing symptoms with basic time patterns. Lower part: corresponding statistical evaluation of basic time patterns ("frequency plots"). Note that the bars in the symptom log are composed of dots, one dot for each day during which the symptom was experienced. The dots are graphically not resolved in this plot. Vertical lines in frequency plots have 4 week distance, the Borrelia burgdorferi reference flare cycle after J.J. Burrascano.
The characteristics of the model symptoms are:
- Symptom 1 occurs in cycles of 28 days length ("flare cycles"), the reference flare cycle according to Burrascano.
- Symptom 2 occurs every day (no cycles).
- Symptom 3 occurs in 2 sets of cycles of 28 days length, with a phase shift at their intersection:
- first part: 3.5 cycles,
- second part: 2.5 cycles.
- Symptom 4 occurs in cycles first, and then continuously.
- Symptom 5 occurs at random.
- Symptom 6 occurs continuously during two time spans, with no symptom occurrence in between these times.
- Symptom 7 is similar to symptom 1 in that it appears basically in cycles of 28 days duration. But in distinction to symptom 1, random days during flares are symptom free.
- Symptom 8: Symptom "tapers off", i.e. initially it occurrs every day, then after day 50 basically every other day, but with random symptom free days.
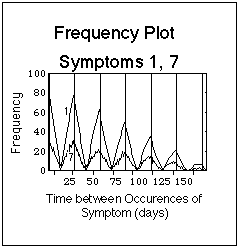
To construct the corresponding frequency plot (lower part of Fig. VIII. 3), we basically counted, for each symptom, how often we found a given vertical distance (time difference) between the dots in the symptom log. This was done with a Mathematica program. The results of these calculations were then displayed in a plot: the frequency of appearance was used as y-value, the corresponding time difference as x-value. To be specific, in the model symptom log we found a time difference of 28 days 75 times. Thus, we entered a point at (x = 28 days, y = 75) in the model frequency plot. Similarly, we found that 60 points in the symptom log are 56 days apart, which lead to the point (x = 56, y = 60). The entire frequency plot has been composed of points this way.
VIII. 4. Comparison of Flare and Menstrual Cycles
VIII 3.2.1 Data
With the help of the next three figures the correlation between symptom and menstrual cycles will be investigated and interpreted.
Fig. VIII 3.1 is the symptom log with the menses cycles superimposed. The menstruation cycles starting at days -2, 21, 45, 68, 186 and 210 have not been recorded and were extra- and interpolated using the average menses cycle of 23.7 days, the latter number being calculated based on the recorded data.
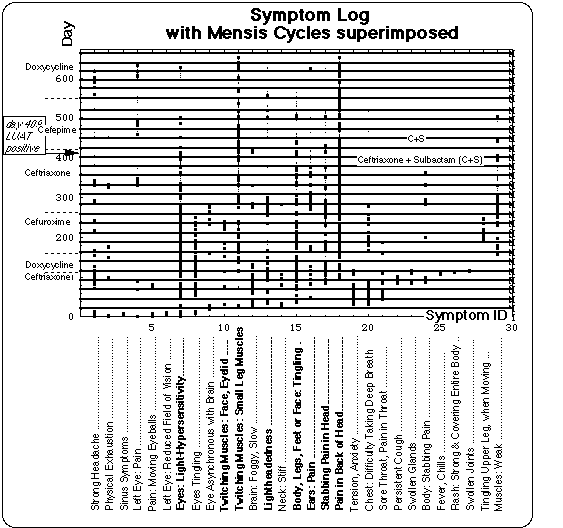
Fig. VIII 3.1: Symptom log (Fig. 1) superimposed on grid of lines marking the days of the onset of the menstrual bleeding. The antibiotics regimens are denoted on the left and right margins of the figure.
A correlation between menstrual cycle and symptom occurrence becomes more visible when this symptom log is
- cut along the lines marking the day of the onset of the menstrual bleeding,
- decomposed into logs of single symptoms and then
- reassembled aligning the days of the onset of the menstrual bleeding.
This has been done in Figs. VIII 3.2 and VIII 3.3.
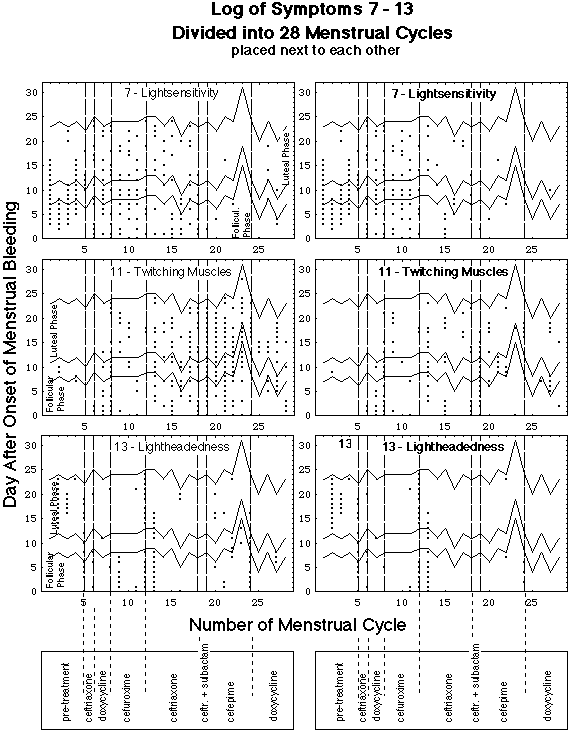
Fig. VIII 3.2: Location of symptomatic days within menstrual cycles: symptom 7 (light-hypersensitivity), 11 {twitching muscles), 13 (lightheadedness). x-axis: number of menstrual cycle, y-axis: day after the onset of menstrual bleeding. A point at coordinates x, y means: symptom appeared on day y of menstrual cycle x, i.e. on day y + delta1 + delta2 + ... deltax-1, where deltai is the length of the ith menstrual cycle. Cycle 1 starts on day - 2 of the symptom log (see Fig. VIII 3.1). Antibiotic regimens are indicated in box below x-axes, dashed lines marking the beginnings of the regimens. Number in upper left corner of diagram is symptom id. Diagram with plain face symptom id: data of complete symptom log (light and heavy dots in Fig. 1), diagram with bold face symptom id: occurrence of symptoms with subthreshold severity deleted (heavy dots in Fig. 1).
Meaning of zig-zag lines:
- The two lowest horizontal zig-zag lines in each diagram mark the limits of ovulation time.
- The uppermost zig-zag line marks the end of the menstrual period.
Menstrual phases:
- The time below the two lowest lines is the follicular phase.
- The time after the ovulation is the luteal phase.
- The 6 days time period, consisting of approximately 3 days before the menses (below the uppermost zig-zag line) and approximately 3 days after the menses (day 0), is called Immune Response Interval. M.S. Barkley observed an intensification of symptoms in this phase.
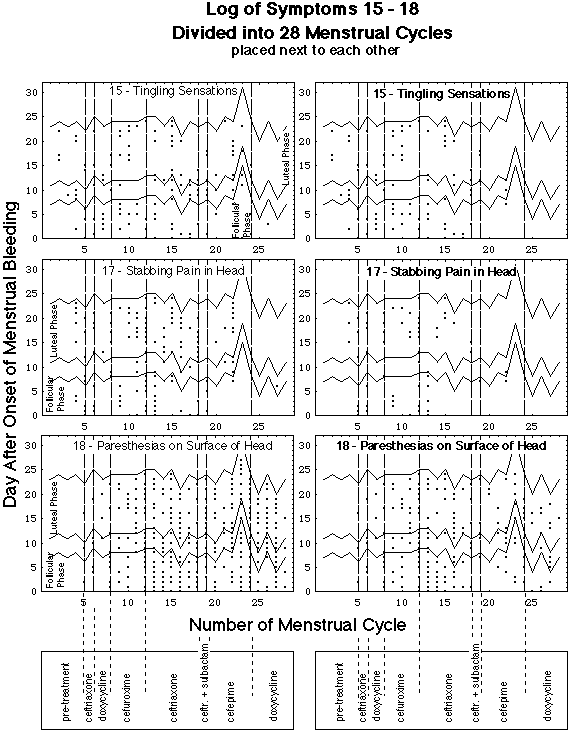
Fig. VIII 3.3: Location of symptomatic days within menstrual cycles: symptom 15 (tingling sensations), 17 (stabbing pain in head) and 18 (paresthesias in the head). See also caption of Fig. VIII 3.2
The statistical analysis displayed in Figs. 2, 3, 4, 5 has shown immune system oscillations in mid disease (i.e. during days 150 ... 350 which correspond to menstrual cycles 7 ... 15), having flare cycle durations that depend on parameters such as type of symptom and antibiotic. With the help of a model of the immune system, this has been interpreted as an indication of the severity of the infection: In the attempt to control the high antigen concentrations the immune system gets locked into undamped feedback control oscillations. The model suggests that further parameters influencing amplitudes and frequencies of the oscillations are concentration thresholds, lag phases, and the spirochete generation time or leak rates r(t) of the toxins from the niches housing them.
Contrary to these oscillations which the immune system establishes by itself, Figs. VIII 3.2 and 3 show that
- in the beginning of the disease most symptoms start in the follicular phase (regular rectangles),
- in late disease, after a long period of antibiosis, the symptoms cluster in the luteal phase (round-cornered rectangles).
These symptom cycles might reflect immune system modulation by the component of the endocrine system that is responsible for the menstruation cycle (immuno-modulation: Groer et al. 1993, Northern et al. 1994, Lyme disease symptoms clustering in luteal phase: Bleiweiss, Bransfield):
- Beginning of the infection:
Because of their long in vivo generation time, Bb will multiply slowly and the female immune system is likely to first register their presence when the immune system's activity is high, i.e. in the follicular phase. This is supported by the observation of Barkley, Harris and Szantyr, who observed systematically high Bb specific antigen concentrations in the urine of a Lyme patient (Barkley et al., 1997) during this phase.
- Late disease after long periods of antibiotics:
As we did for the self-organized immune system oscillations, let us assume a more or less constant flux of mito- and immunogenic toxins from niches into the compartments responsible for the symptoms. When during the antibiosis the flux decreases to small enough values, the immune system will leave the self-organized oscillatory mode. Then, there are at least two mechanisms that could be responsible for the clustering of symptoms in the luteal phase. The basis for both mechanisms is again the short incubation time of the toxin LPS or Osp: the memory of the immune system is not able to efficiently counteract stimuli towards tissue inflammation, and so the symptoms' frequency and severity follows closely any short term variation of toxin or immune mediator levels.
- The level of the proinflammatory prostaglandin PGE2 is higher in the luteal than in the follicular phase (Leslie et al 1994). The variation with time of the frequency and severity of symptoms might mirror the variation of this inflammation mediator.
- The activity of the immune system removing toxins is lower in the luteal than in the follicular phase, as has been observed by Barkley, Harris and Szantyr (mentioned above). The rate of toxin removal and thus the toxin level will then vary over the menstrual cycle and so will the inflammatory reaction against the toxins.
Thus, clustering of symptoms in the luteal phase might indicate a transition of the disease from an active infection to a post-infection syndrome which will disappear once the immune system has finished cleaning up the niches from residual toxins.
Summary:
Graphical representation of our immune response model.
VIII. 5. Pharmacokinetic Models Used in the Calculations
VIII. 5.1. Cefuroxime Model
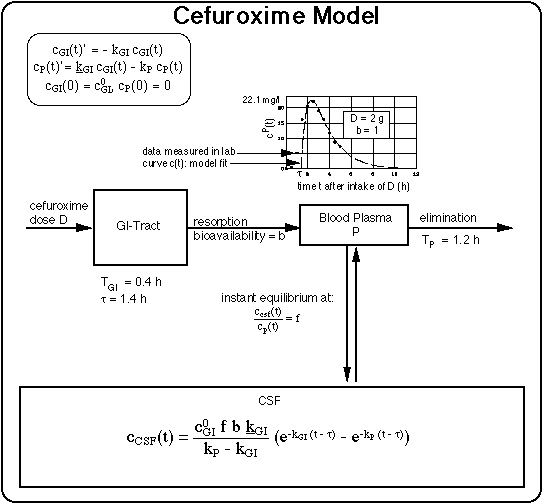
Fig. VIII. 5.1: Pharmacokinetics model used to calculate cefuroxime concentration in CSF. Corresponding set of linear differential equations is shown in top round cornered rectangle. Equation in CSF compartment is analytical solution to this set.
Notation: kGI = kGI multiplied with ratio of volumes of distribution in GI-tract and plasma.
By fitting ccsf(t) to the experimentally determined points, this ratio is automatically assigned its value. For concentrations, rate constants ki = ln2/Ti see Notation Section.
The points in the diagram above the blood plasma compartment are experimentally determined cefuroxime concentrations in the patient's plasma after intake of 2 gram of cefuroxime after a meal. The curve is the model fit. CSF compartment is assumed to be at instant equilibrium with plasma compartment, i.e. the half life of csf compartment is assumed to be T3 < 1 hour.
Data
- Model parameters TGI, TP and tau were adapted so that calculated cP(t) fitted concentrations of cefuroxime measured in patient's blood plasma after intake of the following doses (for more details see Table 3):
- 0.5 gram per intake, 1 intake per day,
- 2 gram per intake, 1 intake per day,
- 2 gram per intake, 2 intakes per day,
- 3 gram per intake, 2 intakes per day,
- 5 gram per intake, 2 intakes per day,
- 2 gram per intake, 2 intakes per day.
- b= 1/2.7 without prior food intake, b = 1 with prior food intake.
- D = dosage of cefuroxime.
- f = 1 for plasma, f = 0.1 for CSF (from "Goodman & Gilman's The Pharmacologic Basis of Therapeutics", 9th ed. (1995), page 1094.
- TGI = 0.4 h, fitted from experimentally determined plasma concentrations for the above doses.
- TP = 1.4 h, fitted from experimentally determined plasma concentrations.
- tau = 1.4 h, fitted from experimentally determined plasma concentrations.
- 22.1 mg/l = peak plasma concentration (total cefuroxime) measured in plasma of patient after intake of 2 gram of cefuroxime with prior meal.
VIII. 5.2. Ceftriaxone Model
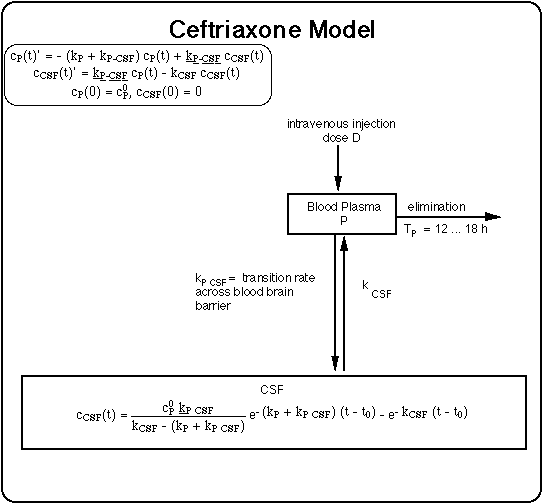
Fig. VIII. 5.2: Pharmacokinetics model used to calculate ceftriaxone concentration in CSF. Corresponding linear set of differential equations is shown in top of Figure. Equation in CSF compartment is analytical solution to this set. Notation: definition of underlined rate constant is analogous to the one given in caption of Fig. VIII. 5.1. For concentrations, rate constants k, t0 see Notation section.
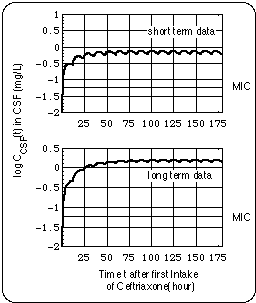
Fig. VIII. 5.3: Ceftriaxone concentrations in CSF for infusion of 1 g ceftriaxone every 12 hours, calculated with the above given pharmacokinetic model and the two sets of parameters described below. Upper diagram: calculations with the parameters fitting the short term data of Nau et al., lower diagram: correspondingly for long term data of Nau et al..
VIII. 5.2.1 Determination of Model Parameters for Ceftriaxone Model
The ceftriaxone concentrations determined in the cerebrospinal fluid of patients with uninflamed meninges by Nau et al. (1993) were re-fitted with the ceftriaxone model in Fig. VIII. 5.2. Two sets of data were presented in the publication:
Fig. VIII. 5.4 shows data (points), fits (curves) and paramters. Note: There is some ambiguity as to the range in which to keep the paramters during optimization. Since error bars are not published, this could not be resolved.
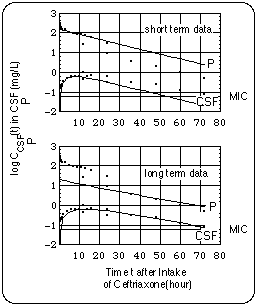
Fig. VIII. 5.4: Fit of pharmacokinetic model (curves) to reproduce total ceftriaxone concentrations (points) published by Nau et al.(1993). Amount of ceftriaxone infused into vein: 2 g. Upper curves in diagrams: concentration in plasma, lower curves in diagrams: concentrations in CSF.
Resulting model paramters fitting the data are (with plasma compartment denoted as compartment 1 and CSF compartment as compartment 2):
- Short term data:
- cP(0) = 150 mg/L after 2 g i.v.,
- T1 = Tp = 12 h,
- T2 = ln2/kcsf = 3 h,
- k12 = kp csf = 0.0015 h-1.
- long term data:
- cP(0) = 20 mg/L after 2 g i.v.,
- T1 = Tp = 15 h,
- T2 = ln2/kcsf = 6 h,
- k12 = kp csf = 0.007 h-1.
VIII. 5.3. Cefepime Model
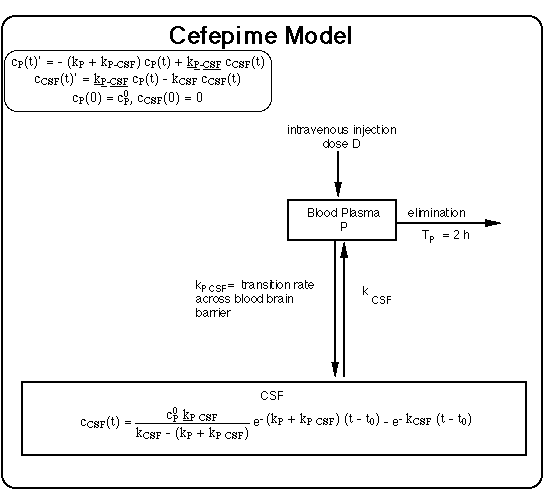
Fig. VIII. 5.5: Model for cefepime pharmacokinetics used to calculate cefepime concentration in CSF. Corresponding linear set of differential equations is shown in top of Figure. Equation in CSF compartment is analytical solution to this set. Notation: See caption of Fig. VIII. 5.2. For concentrations, rate constants k, t0 see Notation section.
VIII. 5.3.1 Determination of Model Parameters for Cefepime Model
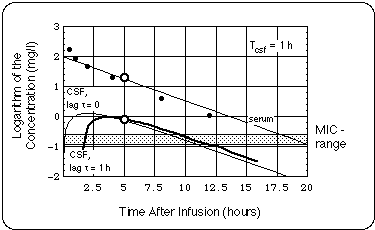
Fig. VIII. 5.6: Fit of pharmacokinetic model (curves) to reproduce total cefepime concentrations in serum and CSF (points and circles). Elimination half life of CSF compartment is Tcsf = ln2/kcsf = 1 hour. Time dependent levels in CSF were calculated for two lag times: tau = 0 (light curve) and tau = 1 h (heavy curve). Points: data published in Bristol Myers Squibb Cefepime Presciption Information. Circles: two samples taken on day 416, i.e. after 6 infusions of 2 g cefepime each, distance between infusions: 8 h, samples were drawn 5 h after last infusion. Upper circle: level in serum (19 mg/L, measurement error: 5 %), lower circle: level in CSF (0.75 mg/L, measurement error: < 10 %, detection limit: 0.1 mg/L). Samples courtesy of Dr. Patricia Coyle, Department of Neurology, State University of New York, Stony Brook, N.Y. 11794, USA. HPLC determination of levels in samples courtesy of Dr. Herman Mattie, Department of Infectious Diseases, Leiden University Medical Center, NL - 2300 RC Leiden, The Netherlands.
The model paramters used in the pharmacokinetic calculations are
- TP = 2.0 h ,
- cP(0) = 100 mg/L (corresponding to 2 g i.v).
- TCSF = ln2/kCSF = 1.0 h. (D. Wagner suspects TCSF > TP, thus cefepime accumulating in the CSF).
- kP CSF = 0.018 h-1,
- tau = 0 and 1 h,
where data from Bristol Myers Squibb have been printed in plain font, and the data from model fit shown in Fig. VIII. 5.6 in underlined font. Bold face values denote the conservative estimate.
Note that the tau = 1 case (heavy curve) results in a higher post peak concentration in the CSF as the tau = 0 case (light curve). The latter fit will thus be called a "conservative estimate".
Fig. VIII. 5.7 shows a fit of the data with the same values for TP = 2.0 h and cP(0) = 100 mg/L
- a longer elimination half life TCSF = 2.0 h, i.e. for a slight accumulation of cefepime in the CSF,
- a correspondingly adjusted rate constant kP CSF = 0.009 h-1, and
- tau = 0 and 1 h.
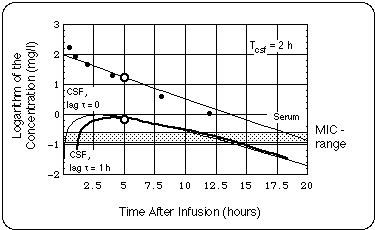
Fig. VIII. 5.7: Fit of pharmacokinetic model (curves) to reproduce total cefepime concentrations in serum and CSF (points and circles). Elimination half life of CSF compartment is Tcsf = ln2/kcsf = 2 hours, otherwise data and notation as in Fig. VIII. 5.6.
Note that this fit of data results in a higher cefepime concentration in the CSF than the fit for TCSF = 1.0 h. The same is true for the tau = 1 h fit here as with the previous set of parameters (Figs. VIII.5. 6 and 7). Thus, the fit with
is the most conservative estimate, and it will therefore be used in the calculation of the necessary dosage.
VIII. 5.3.2 Minimum Inhibitory Concentration for Cefepime
Because reliable data of the minimum inhibitory cefepime concentration (MIC) for Borrelia burgdorferi are missing, alongside with two MIC's provided by Bristol-Myers Squibb (0.12 mg/L and 0.26 mg/L) a probable MIC has to be extracted from
Fig. VIII. 5.8: Systematics of MIC90's for a range of antibiotics (horizontal axis) and gram negative bacilli. Vertical axis: logarithm of MIC, MIC measured in mg/L.Classification ("penicillin susceptible", etc) from Spangler 1997).
The beta-lactam antibiotics used in this systematics consist of one carbapenem (imipenem) and 4 cephalosporins. For the listed bacteria, the MIC of cefepime is generally more than a factor of 2 smaller than the MIC of the rest of the cephalosporins, an exception being Moraxella catarrhalis. The systematics shows that the data from Bristol-Myers Squibb and Preac-Mursic et al. are basically consistent.
In the following evaluations the MIC range (0.12 mg/L and 0.26 mg/L) provided by Bristol-Myers Squibb will be used.
After these pharmacokinetic calculations had been finished, Dever et al. 1999 published the following value for Bb strain B31: MICB31 for cefepime = 1 mg/L.
VIII. 5.3.3 Necessary Cefepime Regimen
Fig. VIII. 5.9 shows the cefepime concentrations in the CSF when 2 grams of the drug are infused every 8 or 12 hours. The calculations were done with the conservative set of parameters.
Fig. VIII. 5.9: Cefepime concentrations in CSF for intravenous infusion of 2 g cefepime every 8 and 12 hours, respectively, calculated with the above given pharmacokinetic model and parameters. Shaded area: range of Minimum Inhibitory Concentration (MIC). Note that in July 1999 Dever et al. published a MIC value for Bb strain B31: MICB31 = 1 mg/L.
When 2 grams of cefepime are infused only every 12 hours, the concentration in the CSF falls below the range 0.26 ... 0.12 mg/L in which the Minimum Inhibitory Concentration for Bb is expected to lie. When the interval between infusions is 8 hours, the cefepime level stays well above that range.
Thus, in summary, infusion of 2 grams cefepime every 8 hours appears necessary in view of the scarcity of the available data.
VIII. 5.4. Dosage of Doxycycline
Doxycycline has a serum elimination half life of (20 ± 5) h (Shmuklarsky et al. 1994, Rx-List, see also Doxycycline, in Mosby's GenRx, 1998).
Figure VIII.5.4.1: Following a 200 mg dose of doxycycline monohydrate, 24 normal adult volunteers averaged these serum concentration values. Maximum concentration: 3.61 mg/L (± 0.9 sd), time of maximum concentration: 2.6 hr (± 1.10 sd), elimination rate constant: 0.049 per hr (± 0.030 sd), half-life: 16.33 hr (± 4.53 sd)
Source: Monodox (Doxycycline) Drug Information: Clinical Pharmacology, Prescribing Information at RxList (2015) (in cache).
|
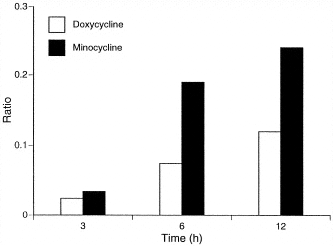
Fig. VIII.5.4.2: Ratio of CSF to serum concentrations of doxycycline and minocycline after multiple 100-mg oral doses given twice daily. Data from Macdonald H, Kelly RG, Allen S, Noble JF, Kanegis LA. Pharmacokinetic studies on minocycline in man. Clin Pharmacol Ther 1973;14:852-61.
|
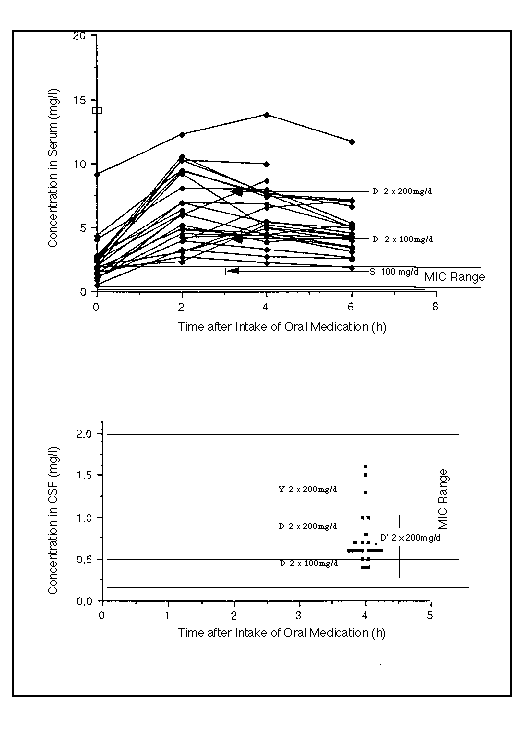
Fig. VIII. 5.10: Doxycycline concentrations in serum (upper plot) and CSF (lower plot) (units: mg/L), as determined
- by Karlsson et al. 1989 (26 patients, intake of 200 mg doxycycline per day for 13 days prior to measurement, points),
- by Dotevall et al. 1989
(12 patients, intake of 2 x 100 mg doxycycline per day for 5 ... 8 days prior to measurement, D represents mean of 12 patients), and
(10 patients, intake of 2 x 200 mg doxycycline per day for 5 ... 8 days prior to measurement, D represents mean of 10 patients),
- by Dotevall et al. 1988 (9 patients, intake of 2 x 200 mg doxycycline per day for 5 days prior to measurement, D' represents range of 9 patients) and
- by Yim et al. 1985 (5 patients, intake of 2 x 200 mg doxycycline per day for 3.5 days prior to measurement, Y represents mean of 5 patients).
- by Shmuklarsky et al. 1994 (13 patients, intake of 1 x 100 mg doxycycline per day for 3 days prior to measurement, S and the associated error bar represents mean and standard deviation, respectively, of 13 patients).
- in serum of the 43-year old woman investigated in this study, on day 591, 12 hours after last doxycycline intake (3 times 200 mg per day for 30 days). Doxycycline level is 14 mg/L (rectangle on y-axis).
Plot Axes
- x-axis: time after intake of last tablet,
- y-axis: concentration.
Lines
Data
- Data by Karlsson et al. are represented as points,
- all other data are represented by the location of the text within the two plots.
- The locations of the points in the scattergram (CSF) and the lines (in the graph for the serum) are not correlated (Karlsson et al. 1989).
Dose:
Assuming a linear dose/concentration relationship, an intake of the 3 x 200 mg recommended by Burrascano would result in the following ranges of the mean CSF levels
- 1.2 ... 5.1 mg/L (data by Karlsson, 1989),
- 1.7 ... 1.8 mg/L (data by Dotevall, 1989),
- 0.3 ... 1.5 mg/L (data by Dotevall, 1988),
- 2.0 mg/L (data by Yim, 1985).
Treatment duration:
Sam Donta has clearly shown that at least three months of therapy with the tetracyclines is needed to even begin an adequate response.
Of related interest:
Review and several examples of proven borrelia treatment failures on standard doxycycline dosage in
Lee J, Wormser GP., Pharmacodynamics of doxycycline for chemoprophylaxis of Lyme disease: preliminary findings and possible implications for other antimicrobials. Int J Antimicrob Agents. 2008 Mar;31(3):235-9.
Cunha Burke A., Minocycline versus Doxycycline in the Treatment of LymeNeuoborreliosis, Clin Infect Dis. (2000) 30 (1): 237-238. doi: 10.1086/313604 (cached)
version: 29 August 2017
Address of this document.
Home.
Send comments to Joachim Gruber.